
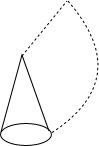
 (1)已知圆锥的底面半径为2cm,母线长为4cm,求圆锥的表面积;
(1)已知圆锥的底面半径为2cm,母线长为4cm,求圆锥的表面积;分析 (1)先利用圆锥的侧面展开图为一扇形,这个扇形的弧长等于圆锥底面的周长,扇形的半径等于圆锥的母线长和扇形面积公式计算出侧面积,然后加上底面积即可得到圆锥的表面积;
(2)利用圆锥的侧面展开图为一扇形,所以扇形面积公式计算即可得到圆锥的侧面积;
(3)设圆锥的母线长为R,利用圆锥的侧面展开图为一扇形,这个扇形的弧长等于圆锥底面的周长,扇形的半径等于圆锥的母线长和扇形面积公式得$\frac{1}{2}$•2π•3•R=15π,解得R=5,然后利用勾股定理计算圆锥的高.
解答 解:(1)圆锥的表面积=π•22+$\frac{1}{2}$•2π•2•4=12π(cm2);
(2)圆锥的侧面积=$\frac{90•π•{6}^{2}}{360}$=9π(cm2);
(3)设圆锥的母线长为R,
根据题意得$\frac{1}{2}$•2π•3•R=15π,解得R=5,
所以圆锥的高=$\sqrt{{5}^{2}-{3}^{2}}$=4.
点评 本题考查了圆锥的计算:圆锥的侧面展开图为一扇形,这个扇形的弧长等于圆锥底面的周长,扇形的半径等于圆锥的母线长.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
 如图把一个转盘分成四等分依次标上数字1、2、3、4,若连续自由转动转盘两次,指针指向的数字分别记得a、b,作为点的横、纵坐标,
如图把一个转盘分成四等分依次标上数字1、2、3、4,若连续自由转动转盘两次,指针指向的数字分别记得a、b,作为点的横、纵坐标,查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 己知数轴上顺次有A,B,C三点,分别表示数a,b,c,并且满足(a+24)2+|b+10|=0,b与c互为相反数,两只电子小蜗牛甲、乙分别从A,C两点同时相向而行,甲的速度为2个单位/秒,乙的速度为6个单位/秒.
己知数轴上顺次有A,B,C三点,分别表示数a,b,c,并且满足(a+24)2+|b+10|=0,b与c互为相反数,两只电子小蜗牛甲、乙分别从A,C两点同时相向而行,甲的速度为2个单位/秒,乙的速度为6个单位/秒.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com