
【题目】如图1所示的是午休时老师们所用的一种折叠椅,现将躺椅以如图2所示的方式倾斜放置,AM与地面ME成45°角,AB∥ME,椅背BC与水平线成30°角,其中AM=50厘米,BC=72厘米,BP是躺椅的伸缩支架,且30°≤BPM≤90°.(结果精确到1厘米;参考数据![]() ≈1.4,
≈1.4,![]() ≈ 1.7,
≈ 1.7,![]() ≈ 2.2)
≈ 2.2)

(1)求此时点C与地面的距离.
(2)在(1)的条件下,求伸缩支架BP可达到的最大值.
【答案】(1)此时点C与地面的距离是71厘米;(2)伸缩支架BP可达到的最大值是70厘米.
【解析】
(1)根据题意和图象,利用锐角三角函数可以解答本题;
(2)根据(1)中的条件和图形,可以求得伸缩支架BP可达到的最大值.
解:(1)∵AM与地面ME成45°角,AB∥ME,椅背BC与水平线成30°角,其中AM=50厘米,BC=72厘米,
∴点A到地面的距离为:AMsins45°=50×![]() =25
=25![]() (厘米),
(厘米),
CD=BCsin30°=72×![]() =36(厘米),
=36(厘米),
∴点C与地面的距离是:25![]() +36≈71(厘米),
+36≈71(厘米),
即此时点C与地面的距离是71厘米;
(2)∵AB∥ME,
∴点B到ME的距离是25![]() 厘米,
厘米,
∴BP=![]() ,
,
∵30°≤BPM≤90°,
∴当∠MPM=30°时,
BP取得最大值,此时BP=![]() =50
=50![]() ≈70(厘米),
≈70(厘米),
即伸缩支架BP可达到的最大值是70厘米.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
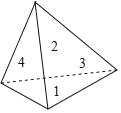
【题目】在学校开展的数学活动课上,小明和小刚制作了一个正三棱锥(质量均匀,四个面完全相同),并在各个面上分别标记数字1,2,3,4,游戏规则如下:每人投掷三棱锥一次,并记录底面的数字,如果底面数字的和为奇数,那么小明赢;如果底面数字的和为偶数,那么小刚赢.
(1)请用列表或画树状图的方法表示上述游戏中的所有可能结果.
(2)请分别求出小明和小刚能赢的概率,并判断此游戏对双方是否公平.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD为矩形,AB=4cm,AD=3cm,动点M,N分别从点D,B同时出发,都以1cm/s的速度运动.点M沿DA向终点A运动,点N沿BC向终点C运动.过点N作NP⊥BC,交AC于点O,连接MP.已知动点运动了ts(0<t<3).
(1)当t为多少时,PM∥AB?
(2)若四边形CDMP的面积为S,试求S与t的函数关系式.
(3)在运动过程中,是否存在某一时刻t使四边形CDMP面积与四边形ABCD面积比为3:8?若存在,请求出t的值;若不存在,请说明理由.
(4)在点M,N运动过程中,△MPA能否成为一个等腰三角形?若能,求出所有可能的t值;若不能,试说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2﹣5ax+c与坐标轴分别交于点A,C,E三点,其中A(﹣3,0),C(0,4),点B在x轴上,AC=BC,过点B作BD⊥x轴交抛物线于点D,点M,N分别是线段CO,BC上的动点,且CM=BN,连接MN,AM,AN.
(1)求抛物线的解析式及点D的坐标;
(2)当△CMN是直角三角形时,求点M的坐标;
(3)试求出AM+AN的最小值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是小强洗漱时的侧面示意图,洗漱台(矩形ABCD)靠墙摆放,高AD=80cm,宽AB=48cm,小强身高166cm,下半身FG=100cm,洗漱时下半身与地面成80°(∠FGK=80°),身体前倾成125°(∠EFG=125°),脚与洗漱台距离GC=15cm(点D,C,G,K在同一直线上).
(1)此时小强头部E点与地面DK相距多少?
(2)小强希望他的头部E恰好在洗漱盆AB的中点O的正上方,他应向前或后退多少?
(sin80°≈0.98,cos80°≈0.17, ![]() ≈1.41,结果精确到0.1cm)
≈1.41,结果精确到0.1cm)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,是一种斜挎包,其挎带由双层部分、单层部分和调节扣构成.小敏用后发现,通过调节扣加长或缩短单层部分的长度,可以使挎带的长度(单层部分与双层部分长度的和,其中调节扣所占的长度忽略不计)加长或缩短.设单层部分的长度为![]() ,双层部分的长度为
,双层部分的长度为![]() ,经测量,得到如下数据:
,经测量,得到如下数据:
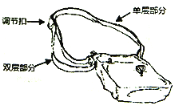

(1)求出![]() 关于
关于![]() 的函数解析式,并求当
的函数解析式,并求当![]() 时
时![]() 的值;
的值;
(2)根据小敏的身高和习惯,挎带的长度为![]() 时,背起来正合适,请求出此时单层部分的长度;
时,背起来正合适,请求出此时单层部分的长度;
(3)设挎带的长度为![]() ,求
,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“绿水青山就是金山银山”,为保护生态环境,A,B两村准备各自清理所属区域养鱼网箱和捕鱼网箱,每村参加清理人数及总开支如下表:
村庄 | 清理养鱼网箱人数/人 | 清理捕鱼网箱人数/人 | 总支出/元 |
A | 15 | 9 | 57000 |
B | 10 | 16 | 68000 |
(1)若两村清理同类渔具的人均支出费用一样,求清理养鱼网箱和捕鱼网箱的人均支出费用各是多少元;
(2)在人均支出费用不变的情况下,为节约开支,两村准备抽调40人共同清理养鱼网箱和捕鱼网箱,要使总支出不超过102000元,且清理养鱼网箱人数小于清理捕鱼网箱人数,则有哪几种分配清理人员方案?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com