解:(1)①线段DT、DS的数量和位置关系分别是:DT=DS,DT⊥DS.理由如下:
∵AC为正方形ABCD的对角线,
∴∠TAD=45°,
∵TS为直径,
∴∠SDT=90°,
又∵∠TSD=∠TAD,
∴∠TSD=45°,
∴△DST为等腰直角三角形,
∴DT=DS,DT⊥DS;
②∵∠SDT=∠ADC=90°,
∴∠SDA=∠CDT,
又∵TS为直径,
∴∠SAT=90°,
∴∠SAD=45°,
∴∠SAD=∠DCT,
而DA=DC,
∴△DAS≌△DCT,
∴AS=TC,
∴AS+AT=AC,
而正方形ABCD的边长为4,
∴AC=4

,
∴AS+AT=

;
(2)∵TS为直径,
∴∠SAT=90°,∠SDT=90°,
∴∠SAC=90°,
而∠CAD=45°,
∴∠SAD=45°,
∴∠STD=45°,
∴△DST为等腰直角三角形,
∴DS=DT,
又∵∠SAD=∠DCT=45°,∠ASD=∠DTC,
∴△DAS≌△DCT,
∴AS=TC,
∴AS-AT=TC-AT=AC=

;
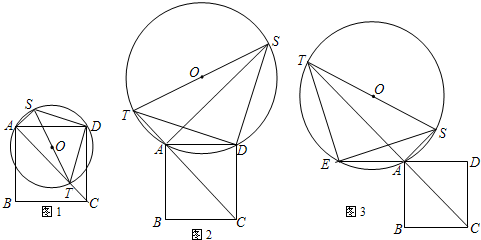
(3)提出的问题是:求 AT-AS 的值.
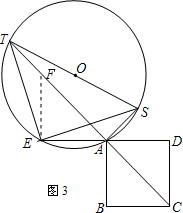
解答如下:
在TA上截取TF=AS,连接EF,如图,
∵∠TAE=∠BAC=45°,
∴△EST为等腰直角三角形,
∴SE=TE,
又∵∠ASE=∠ETF,
在△EAS和△EFT中,
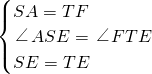
∴△EAS≌△EFT(SAS),
∴∠SEA=∠TEF,AE=EF,
而∠TES=90°,
∴∠AEF=90°,
∴△AEF为等腰直角三角形,
∴AF=

AE,
∵AE=AD=4,
∴AT-AS=AT-TF=AF=

.
分析:(1)①根据正方形的性质得∠TAD=45°,再根据圆周角定理和推论得∠SDT=90°,∠TSD=∠TAD,易得△DST为等腰直角三角形,则DT=DS,DT⊥DS;
②由∠SDT=∠ADC=90°得∠SDA=∠CDT,易证得△DAS≌△DCT,得AS=TC,所以AS-AT=TC-AT=AC=

;
(2)同样可证得△DST为等腰直角三角形,得到DS=DT,而∠SAD=∠DCT=45°,∠ASD=∠DTC,则△DAS≌△DCT,AS=TC,得AS-AT=TC-AT=AC=4

;
(3)提出的问题是:求 AT-AS 的值.在TA上截取TF=AS,连接EF,易证得△EST为等腰直角三角形,得到SE=TE,易证△EAS≌△EFT,得到∠SEA=∠TEF,AE=EF,
得到△AEF为等腰直角三角形,则AF=

AE,而AE=AD=4,于是有AT-AS=AT-TF=AF=

.
点评:本题考查了圆周角定理以及推论:在同圆或等圆中,同弧或等弧所对的圆周角相等;直径所对的圆周角为直角.也考查了正方形的性质以及三角形全等的判定与性质.

 ,
, ;
; ;
; 解答如下:
解答如下: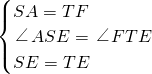
 AE,
AE, .
. ;
; ;
; AE,而AE=AD=4,于是有AT-AS=AT-TF=AF=
AE,而AE=AD=4,于是有AT-AS=AT-TF=AF= .
.

 如图,已知:正方形ABCD边长为1,E、F、G、H分别为各边上的点,且AE=BF=CG=DH,设小正方形EFGH的面积为s,AE为x,则s关于x的函数图象大致是( )
如图,已知:正方形ABCD边长为1,E、F、G、H分别为各边上的点,且AE=BF=CG=DH,设小正方形EFGH的面积为s,AE为x,则s关于x的函数图象大致是( )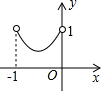
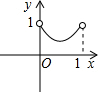
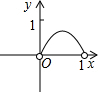
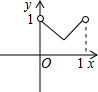
 由.
由. s的速度运动,同时动点Q在线段FC上从F?C以1cm/s的速度运动,动点G在PC上,且∠EGC=∠EQC,连接PD.设运动时间为t秒.
s的速度运动,同时动点Q在线段FC上从F?C以1cm/s的速度运动,动点G在PC上,且∠EGC=∠EQC,连接PD.设运动时间为t秒. 如图,已知在正方形ABCD外取一点E,连接AE、BE、DE.过点A作AE的垂线交DE于点P.若AE=AP=1,PB=
如图,已知在正方形ABCD外取一点E,连接AE、BE、DE.过点A作AE的垂线交DE于点P.若AE=AP=1,PB=