
【题目】如图,在平面直角坐标系内,点![]() 的坐标为(0,24),经过原点的直线
的坐标为(0,24),经过原点的直线![]() 与经过点
与经过点![]() 的直线
的直线![]() 相交于点
相交于点![]() ,点
,点![]() 的坐标为(18,6).
的坐标为(18,6).
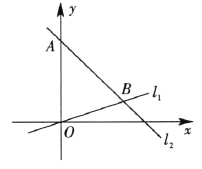
(1)求直线![]() ,
,![]() 对应的函数表达式;
对应的函数表达式;
(2)点![]() 为线段
为线段![]() 上一动点(点
上一动点(点![]() 不与点
不与点![]() 重合),作
重合),作![]() 轴交直线
轴交直线![]() 于点
于点![]() ,设点
,设点![]() 的纵坐标为
的纵坐标为![]() ,求点
,求点![]() 的坐标(用含
的坐标(用含![]() 的代数式表示)
的代数式表示)
【答案】(1)直线l1对应的函数表达式为y=![]() x,直线l2对应的函数表达式为y=-x+24;(2)(3a,-3a+24)
x,直线l2对应的函数表达式为y=-x+24;(2)(3a,-3a+24)
【解析】
(1)根据待定系数法即可求解;
(2)因为点C在直线l1上,且点C的纵坐标为a,所以a=![]() x,得到C点坐标,再根据CD∥y轴,得到点D的横坐标为3a,进而得到D点坐标.
x,得到C点坐标,再根据CD∥y轴,得到点D的横坐标为3a,进而得到D点坐标.
解:(1)设直线l1对应的函数表达式为y=k1x,由它过点(18,6)得18k1=6,
解得k1=![]() ,
,
所以直线l1对应的函数表达式为y=![]() x;
x;
设直线l2对应的函数表达式为y=k2x+b,
由它过点A(0,24),B(18,6)得b=24,18k2+b=6,解得k2=-1,
所以直线l2对应的函数表达式为y=-x+24
(2)因为点C在直线l1上,且点C的纵坐标为a,所以a=![]() x.
x.
所以x=3a,故点C的坐标为(3a,a).
因为CD∥y轴, 所以点D的横坐标为3a.
因为点D在直线l2上,所以点D的纵坐标为-3a+24.
所以点D的坐标为(3a,-3a+24).


科目:初中数学 来源: 题型:
【题目】将正面分别写着数字1,2,3的三张卡片(注:这三张卡片的形状、大小、质地,颜色等其他方面完全相同,若背面上放在桌面上,这三张卡片看上去无任何差别)洗匀后,背面向上放在桌面上,从中先随机抽取一张卡片,记该卡片上的数字为x,再把剩下的两张卡片洗匀后,背面向上放在桌面上,再从这两张卡片中随机抽取一张卡片,记该卡片上的数字为y.
(1)用列表法或树状图法(树状图也称树形图)中的一种方法,写出(x,y)所有可能出现的结果.
(2)求取出的两张卡片上的数字之和为偶数的概率P.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两人分别从A、B两地同时出发,相向而行,匀速前往B地、A地,两人相遇时停留了4min,又各自按原速前往目的地,甲、乙两人之间的距离y(m)与甲所用时间x(min)之间的函数关系如图所示.有下列说法:

①A、B之间的距离为1200m; ②乙行走的速度是甲的1.5倍;③ b=960; ④ a=34.
以上结论正确的有( )
A. ①② B. ①②③ C. ①③④ D. ①②④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校学生会准备调查六年级学生参加“武术类”、“书画类”、“棋牌类”、“器乐类”四类校本课程的人数.
(1)确定调查方式时,甲同学说:“我到六年级(1)班去调查全体同学”;乙同学说:“放学时我到校门口随机调查部分同学”;丙同学说:“我到六年级每个班随机调查一定数量的同学”.请指出哪位同学的调查方式最合理.
类别 | 频数(人数) | 频率 |
武术类 | 0.25 | |
书画类 | 20 | 0.20 |
棋牌类 | 15 | b |
器乐类 | ||
合计 | a | 1.00 |
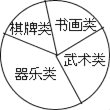
(2)他们采用了最为合理的调查方法收集数据,并绘制了如图所示的统计表和扇形统计图.
请你根据以上图表提供的信息解答下列问题:
①a=_____,b=_____;
②在扇形统计图中,器乐类所对应扇形的圆心角的度数是_____;
③若该校六年级有学生560人,请你估计大约有多少学生参加武术类校本课程.
查看答案和解析>>
科目:初中数学 来源: 题型:
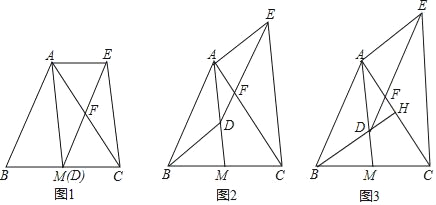
【题目】如图,AM是△ABC的中线,D是线段AM上一点(不与点A重合).DE∥AB交AC于点F,CE∥AM,连结AE.
(1)如图1,当点D与M重合时,求证:四边形ABDE是平行四边形;
(2)如图2,当点D不与M重合时,(1)中的结论还成立吗?请说明理由.
(3)如图3,延长BD交AC于点H,若BH⊥AC,且BH=AM.
①求∠CAM的度数;
②当FH=![]() ,DM=4时,求DH的长.
,DM=4时,求DH的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
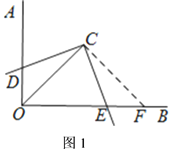
【题目】当你站在博物馆的展览厅中时,你知道站在何处观赏最理想吗?如图,设墙壁上的展品最高点P距地面2.5米,最低点Q距地面2米,观赏者的眼睛F距地面1.6米,当视角∠PEQ最大时,站在此处观赏最理想,则此时E到墙壁的距离为( )米.

A. 1 B. 0.6 C. 0.5 D. 0.4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知![]() 与
与![]() ,
,![]() 平分
平分![]() .
.
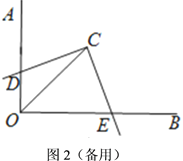
(1)如图1,![]() 与
与![]() 的两边分别相交于点
的两边分别相交于点![]() 、
、![]() ,
,![]() ,试判断线段
,试判断线段![]() 与
与![]() 的数量关系,并说明理由.
的数量关系,并说明理由.
以下是小宇同学给出如下正确的解法:
解:![]() .
.
理由如下:如图1,过点![]() 作
作![]() ,交
,交![]() 于点
于点![]() ,则
,则![]() ,
,
…
请根据小宇同学的证明思路,写出该证明的剩余部分.
(2)你有与小宇不同的思考方法吗?请写出你的证明过程.
(3)若![]() ,
,![]() .
.
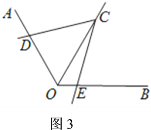
①如图3,![]() 与
与![]() 的两边分别相交于点
的两边分别相交于点![]() 、
、![]() 时,(1)中的结论成立吗?为什么?线段
时,(1)中的结论成立吗?为什么?线段![]() 、
、![]() 、
、![]() 有什么数量关系?说明理由.
有什么数量关系?说明理由.
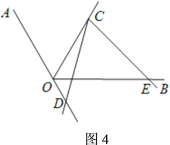
②如图4,![]() 的一边与
的一边与![]() 的延长线相交时,请回答(1)中的结论是否成立,并请直接写出线段
的延长线相交时,请回答(1)中的结论是否成立,并请直接写出线段![]() 、
、![]() 、
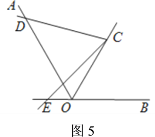
、![]() 有什么数量关系;如图5,
有什么数量关系;如图5,![]() 的一边与
的一边与![]() 的延长线相交时,请回答(1)中的结论是否成立,并请直接写出线段
的延长线相交时,请回答(1)中的结论是否成立,并请直接写出线段![]() 、
、![]() 、
、![]() 有什么数量关系.
有什么数量关系.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,已知△ABC的三个顶点的坐标分别为A(1,0),B(2,﹣3),C(4,﹣2).
(1)画出△ABC关于x轴的对称图形△A1B1C1;
(2)画出△A1B1C1向左平移3个单位长度后得到的△A2B2C2;
(3)如果AC上有一点P(m,n)经过上述两次变换,那么对应A2C2上的点P2的坐标是 .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在四边形ABCD的边BC的延长线上取一点E,在直线BC的同侧作一个以CE为底的等腰△CEF,且满足∠B+∠F=180°,则称三角形CEF为四边形ABCD的“伴随三角形”.
(1)如图1,若△CEF是正方形ABCD的“伴随三角形”:
①连接AC,则∠ACF= ;
②若CE=2BC,连接AE交CF于H,求证:H是CF的中点;
(2)如图2,若△CEF是菱形ABCD的“伴随三角形”,∠B=60°,M是线段AE的中点,连接DM、FM,猜想并证明DM与FM的位置与数量关系.
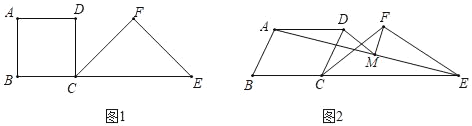
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com