
【题目】若关于x的方程x2﹣2ax+a﹣2=0的一个实数根为x1≥1,另一个实数根x2≤﹣1,则抛物线y=﹣x2+2ax+2﹣a的顶点到x轴距离的最小值是_____.
科目:初中数学 来源: 题型:
【题目】已知关于x的一元二次方程x2+(2m+1)x+m2﹣2=0.
(1)若该方程有两个实数根,求m的最小整数值;
(2)若方程的两个实数根为x1,x2,且(x1﹣x2)2+m2=21,求m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
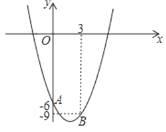
【题目】如图,已知抛物线y=ax2﹣4x+c经过点A(0,﹣6)和B(3,﹣9).
(1)求出抛物线的解析式;
(2)写出抛物线的对称轴方程及顶点坐标;
(3)点P(m,m)与点Q均在抛物线上(其中m>0),且这两点关于抛物线的对称轴对称,求m的值及点Q的坐标;
(4)在满足(3)的情况下,在抛物线的对称轴上寻找一点M,使得△QMA的周长最小.
查看答案和解析>>
科目:初中数学 来源: 题型:
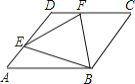
【题目】如图,在边长为1的菱形ABCD中,DAB 60°,E是AD上不同于A,D两点的一动点,F是CD上一点,且AECF1.
(1)证明:无论E,F怎样移动,BEF总是等边三角形;
(2)求BEF 面积的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲班56人,其中身高在160厘米以上的男同学10人,身高在160厘米以上的女同学3人,乙班80人,其中身高在160厘米以上的男同学20人,身高在160厘米以上的女同学8人.如果想在两个班的160厘米以上的女生中抽出一个作为旗手,在哪个班成功的机会大?为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】佳佳向探究一元三次方程x3+2x2﹣x﹣2=0的解的情况,根据以往的学习经验,他想到了方程与函数的关系,一次函数y=kx+b(k≠0)的图象与x轴交点的横坐标即为一元一次方程kx+b(k≠0)的解,二次函数y=ax2+bx+c(a≠0)的图象与x轴交点的横坐标即为一元二次方程ax2+bx+c=0(a≠0)的解,如:二次函数y=x2﹣2x﹣3的图象与x轴的交点为(﹣1,0)和(3,0),交点的横坐标﹣1和3即为x2﹣2x﹣3=0的解.
根据以上方程与函数的关系,如果我们直到函数y=x3+2x2﹣x﹣2的图象与x轴交点的横坐标,即可知方程x3+2x2﹣x﹣2=0的解.
佳佳为了解函数y=x3+2x2﹣x﹣2的图象,通过描点法画出函数的图象.
x | … | ﹣3 | ﹣ | ﹣2 | ﹣ | ﹣1 | ﹣ | 0 |
| 1 |
| 2 | … |
y | … | ﹣8 | ﹣ | 0 |
| m | ﹣ | ﹣2 | ﹣ | 0 |
| 12 | … |
(1)直接写出m的值,并画出函数图象;
(2)根据表格和图象可知,方程的解有 个,分别为 ;
(3)借助函数的图象,直接写出不等式x3+2x2>x+2的解集.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A,B为定点,定直线l//AB,P是l上一动点.点M,N分别为PA,PB的中点,对于下列各值:①线段MN的长;②△PMN的面积;③△PAB的周长;④∠APB的大小;⑤直线MN,AB之间的距离.其中会随点P的移动而不改变的是( )

A. ①②③ B. ①②⑤ C. ②③④ D. ②④⑤
查看答案和解析>>
科目:初中数学 来源: 题型:
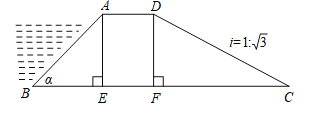
【题目】如图所示,某拦水大坝的横断面为梯形ABCD,AE、DF为梯形的高,其中迎水坡AB的坡角α=45°,坡长AB=![]() 米,背水坡CD的坡度i=1:
米,背水坡CD的坡度i=1:![]() (i为DF与FC的比值),则背水坡CD的坡长为______米.
(i为DF与FC的比值),则背水坡CD的坡长为______米.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲班56人,其中身高在160厘米以上的男同学10人,身高在160厘米以上的女同学3人,乙班80人,其中身高在160厘米以上的男同学20人,身高在160厘米以上的女同学8人.如果想在两个班的160厘米以上的女生中抽出一个作为旗手,在哪个班成功的机会大?为什么?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com