
【题目】如图,在平面直角坐标系中,菱形![]() 的顶点
的顶点![]() 在反比例函数
在反比例函数![]() 图象上,直线
图象上,直线![]() 交
交![]() 于点
于点![]() ,交
,交![]() 正半轴于点
正半轴于点![]() ,且
,且![]()
![]() 求
求![]() 的长:
的长:
![]() 若
若![]() ,求
,求![]() 的值.
的值.
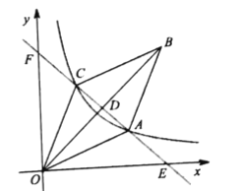
【答案】(1)6;(2)4
【解析】
(1)首先利用勾股定理求出EF的长,然后结合题意利用菱形的性质证明出△DOE为等腰三角形,由此求出DO,最后进一步求解即可;
(2)过点A作AN⊥OE,垂足为E,在Rt△AON中,利用勾股定理求出AN的长,然后进一步根据反比例函数的性质求出![]() 值即可.
值即可.
(1)∵![]() ,
,
∴EF=![]() ,∠OEF=∠OFE=45°,
,∠OEF=∠OFE=45°,
∵四边形OABC为菱形,
∴OA=AB=BC=OC,OB⊥AC,DO=DB,
∴△DOE为等腰三角形,
∴DO=DE=![]() EF=3,
EF=3,
∴OB=2DO=6;
(2)
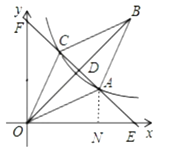
如图,过点A作AN⊥OE,垂足为E,则△ANE为等腰直角三角形,
∴AN=NE,
设AN=![]() ,则NE=
,则NE=![]() ,ON=
,ON=![]() ,
,
在Rt△AON中,由勾股定理可得:![]() ,
,
解得:![]() ,
,![]() ,
,
当![]() 时,A点坐标为:(
时,A点坐标为:(![]() ,
,![]() ),C点坐标为:(
),C点坐标为:(![]() ,
,![]() );
);
当![]() 时,C点坐标为:(
时,C点坐标为:(![]() ,
,![]() ),A点坐标为:(
),A点坐标为:(![]() ,
,![]() );
);
∴![]() .
.


科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD是菱形,对角线AC,BD相交于点O,DH⊥AB于点H,连接OH,若∠DHO=20°,则∠ADC的度数是( )
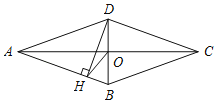
A. 120°B. 130°C. 140°D. 150°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】 在正方形ABCD中.
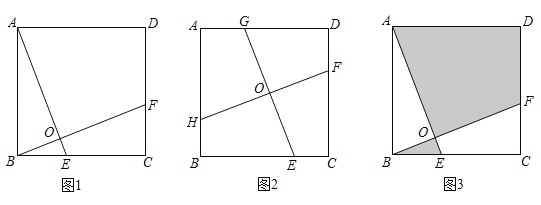
(1)如图1,点E、F分别在BC、CD上,AE、BF相交于点O,∠AOB=90°,试判断AE与BF的数量关系,并说明理由;
(2)如图2,点E、F、G、H分别在边BC、CD、DA、AB上,EG、FH相交于点O,∠GOH=90°,且EG=7,求FH的长;
(3)如图3,点E、F分别在BC、CD上,AE、BF相交于点O,∠AOB=90°,若AB=5,图中阴影部分的面积与正方形的面积之比为4:5,求△ABO的周长.
查看答案和解析>>
科目:初中数学 来源: 题型:
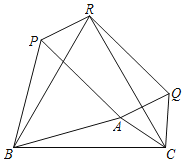
【题目】以△ABC的三边为边在BC的同一侧作等边△ABP,等边△ACQ,等边△BCR.
(1)四边形QRPA是平行四边形吗?若是,请证明;若不是,请说明理由.
(2)当△ABC满足什么条件时,四边形QRPA是矩形?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着移动计算技术和无线网络的快速发展,移动学习方式越来越引起人们的关注.某校计划将这种学习方式应用到教育教学中,从各年级共1500名学生中随机抽取了部分学生,对其家庭中拥有的移动设备情况进行了调查,并绘制出如下的统计图①和图②,根据相关信息,解答下列问题:
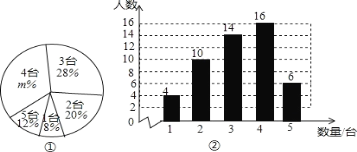
(1)本次接受随机抽样调查的学生人数为 人 ,图①中m的值为 .
(2)求本次调查获取的样本数据的众数、中位数;
(3)根据样本数据,估计该校学生家庭中;拥有3台移动设备的学生人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(本题满分7分)已知关于x的方程![]() 有两个不相等的实数根.
有两个不相等的实数根.
(1)求k的取值范围;
(2)是否存在实数k,使此方程的两个实数根的倒数和等于0?若存在,求出k的值;若不存在,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
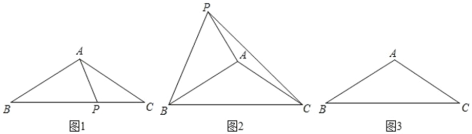
【题目】等腰△ABC 中,AB=AC,∠BAC=120°,点 P 为平面内一点.
(1)如图 1,当点 P 在边 BC 上时,且满足∠APC=120°,求![]() 的值;
的值;
(2)如图 2,当点 P 在△ABC 的外部,且满足∠APC+∠BPC=90°,求证:BP=![]() AP;
AP;
(3)如图 3,点 P 满足∠APC=60°,连接 BP,若 AP=1,PC=3,直接写出BP 的长度.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com