
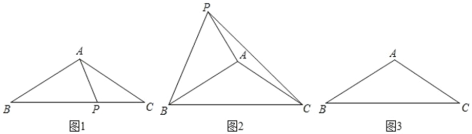
【题目】等腰△ABC 中,AB=AC,∠BAC=120°,点 P 为平面内一点.
(1)如图 1,当点 P 在边 BC 上时,且满足∠APC=120°,求![]() 的值;
的值;
(2)如图 2,当点 P 在△ABC 的外部,且满足∠APC+∠BPC=90°,求证:BP=![]() AP;
AP;
(3)如图 3,点 P 满足∠APC=60°,连接 BP,若 AP=1,PC=3,直接写出BP 的长度.
【答案】(1)2;(2)见解析;(3) 2![]() 或
或![]() .
.
【解析】
(1)由∠BAC=120°,AB=AC,推出∠B=∠C=30°,由∠APC=120°,推出∠PAC=∠C=30°,推出PC=PA,∠PAB=90°,推出PB=2PA,可得 PB=2PC解决问题;
如图 2中,将线段AP绕点 A顺时针旋转120°得到线段AF,连接PF, BF,BF交 PC于点 H.想办法证明PB=PF即可解决问题;
(3)分两种情形分别求解即可解决问题.
(1)如图1中,∵∠BAC=120°,AB=AC,
∴∠B=∠C=30°,
∵∠APC=120°,
∴∠PAC=∠C=30°,
∴PC=PA,∠PAB=90°,
∴PB=2PA,
∴PB=2PC,
∴![]() =2;
=2;
(2)如图2中,将线段AP绕点A顺时针旋转120°得到线段AF,连接PF,BF,BF交PC于点H,
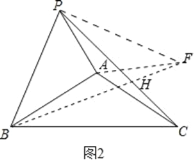
∵∠BAC=∠PAF=120°,
∴∠PAC=∠BAF,
∵AB=AC,AF=AP,
∴△ABF≌△ACP(SAS),
∠APC=∠AFB,
设∠APC=α,则∠AFB=α,∠PFB=30°+α,∠BPC=90°﹣α
∵∠PHB=∠HPF+∠PFH=(30°﹣α)+(30°+α)=60°,
∴∠PBH=180°﹣(90°﹣α﹣60°)=30°+α,
∴∠PBF=∠PFB,
∴PB=PF,
在△PAF中,易知PF=![]() PA,
PA,
∴PB=![]() PA;
PA;
(3)①如图3﹣1中,当点P在△ABC外部时,将线段AP绕点A顺时针旋转 120°得到线段AF,连接PF,BF,
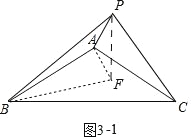
则△ABF≌△ACP(SAS),
∴∠AFB=∠APC=60°,BF=PC=3,
∵∠AFP=30°,
∴∠BFP=90°,
∵PA=AF=1,∠PAF=120°,
∴PF=![]() ,
,
∴PB=![]() =2
=2![]() ;
;
②如图3﹣2中,当点P在△ABC内部时,将线段AP绕点A逆时针旋转120° 得到AH,连接PH,HC.作HM⊥PC于M,
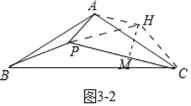
则△BAP≌△CAH(SAS),
∴PB=CH,
∵∠PAH+∠APC=120°+60°=180°,
∴AH∥PC,
∴∠AHP=∠HPM=30°,
∴HM=![]() PH=
PH=![]() ,
,
∴PM=![]() HM=
HM=![]() ,
,
∵PC=3,
∴CM=PM=![]() ,
,
∵HM⊥PC,
∴HC=PH=![]() ,
,
∴PB=![]() ,
,
综上所述,满足条件的 PB 的值为 2![]() 或
或![]() .
.


 世纪百通主体课堂小学课时同步达标系列答案
世纪百通主体课堂小学课时同步达标系列答案 世纪百通优练测系列答案
世纪百通优练测系列答案 百分学生作业本题练王系列答案
百分学生作业本题练王系列答案科目:初中数学 来源: 题型:
【题目】某商店计划购进![]() ,
,![]() 两种型号的电机,其中每台
两种型号的电机,其中每台![]() 型电机的进价比
型电机的进价比![]() 型多
型多![]() 元,且用
元,且用![]() 元购进
元购进![]() 型电机的数量与用
型电机的数量与用![]() 元购进
元购进![]() 型电机的数量相等.
型电机的数量相等.
(1)求![]() ,
,![]() 两种型号电机的进价;
两种型号电机的进价;
(2)该商店打算用不超过![]() 元的资金购进
元的资金购进![]() ,
,![]() 两种型号的电机共
两种型号的电机共![]() 台,至少需要购进多少台
台,至少需要购进多少台![]() 型电机?
型电机?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】现有两个不透明的乒乓球盒,甲盒中装有1个白球和2个红球,乙盒中装有2个白球和若干个红球,这些小球除颜色不同外,其余均相同.若从乙盒中随机摸出一个球,摸到红球的概率为![]() .
.
(1)求乙盒中红球的个数;
(2)若先从甲盒中随机摸出一个球,再从乙盒中随机摸出一个球,请用树形图或列表法求两次摸到不同颜色的球的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
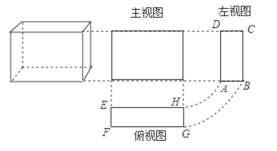
【题目】张师傅根据某几何体零件,按1:1的比例画出准确的三视图(都是长方形)如图,已知EF=4cm,FG=12cm,AD=10cm.
(1)说出这个几何体的名称;
(2)求这个几何体的表面积S;
(3)求这个几何体的体积V.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们知道“距离地面越高,温度越低”,下表给出了距离地面的高度与所在位置的温度之间的大致关系.
距离地面的高度(千米) | 0 | 1 | 2 | 3 | 4 | 5 |
所在位置的温度(C) | 20 | 14 | 8 | 2 |
|
|
(1)上表中哪个是自变量?
(2)由表可知,距离地面高度每上升1千米,温度降低______℃;
(3)2018年5月14日,四川航空3U8633航班执行重庆—拉萨航班任务,飞行途中,在距离地面9800米的高空,驾驶舱右侧挡风玻璃突然破裂,2名飞行员在超低压、超低温的紧急情况下,冷静应对,最终飞机成功降落,创造了世界航空史上的奇迹,请你计算出飞机发生事故时所在高空的温度(假设当时所在位置的地面温度为20℃).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在矩形ABCD中,P为CD边上一点(DP<CP),∠APB=90°.将ΔADP沿AP翻折得到![]() ,PD′的延长线交边AB于点M,过点B作BN‖MP交DC于点N.
,PD′的延长线交边AB于点M,过点B作BN‖MP交DC于点N.
图1
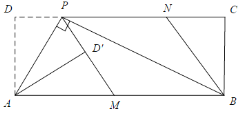
图2
(1)求证:![]() ;
;
(2)请判断四边形PMBN的形状,并说明理由;
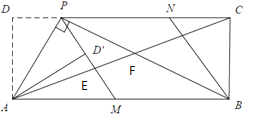
(3)如图2,连接AC,分别交PM,PB于点E,F.若tan∠PAD=![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com