
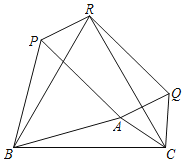
【题目】以△ABC的三边为边在BC的同一侧作等边△ABP,等边△ACQ,等边△BCR.
(1)四边形QRPA是平行四边形吗?若是,请证明;若不是,请说明理由.
(2)当△ABC满足什么条件时,四边形QRPA是矩形?请说明理由.
【答案】(1)四边形QRPA是平行四边形,理由详见解析;(2)当∠BAC=150°时,四边形QRPA是矩形,理由详见解析
【解析】
(1)由“SAS”可证△BRP≌△BCA,△CAB≌△CQR,可得PR=AC,AB=RQ,可得RP=AQ,AP=RQ,可得结论;
(2)当∠BAC=150![]() 时,由周角的性质可求∠PAQ=90
时,由周角的性质可求∠PAQ=90![]() ,可证平行四边形QRPA是矩形.
,可证平行四边形QRPA是矩形.
证明:(1)四边形QRPA是平行四边形
理由如下:∵等边△ABP,等边△ACQ,等边△BCR,
∴AB=PB,BC=BR=CR,AC=CQ,∠PBA=∠RBC=∠BCR=∠ACQ=60![]() ,
,
∴∠PBR=∠ABC,∠ACB=∠QCR,
∴△BRP≌△BCA(SAS),
∴PR=AC,
∵BC=RC,∠BCA=∠RCQ,AC=CQ,
∴△CAB≌△CQR(SAS)
∴AB=RQ,
∴RP=AQ,AP=RQ,
∴四边形QRPA是平行四边形;
(2)当∠BAC=150![]() 时,四边形QRPA是矩形,
时,四边形QRPA是矩形,
∵∠PAQ+∠BAP+∠CAQ+∠BAC=360![]() ,
,
∴∠PAQ=360![]() ﹣60
﹣60![]() ﹣60
﹣60![]() ﹣150
﹣150![]() =90
=90![]() ,
,
∴平行四边形QRPA是矩形.


科目:初中数学 来源: 题型:
【题目】小明坐于堤边垂钓,如图①,河堤AC的坡角为30°,AC长![]() 米,钓竿AO的倾斜角是60°,其长为3米,若AO与钓鱼线OB的夹角为60°,求浮漂B与河堤下端C之间的距离(如图②).
米,钓竿AO的倾斜角是60°,其长为3米,若AO与钓鱼线OB的夹角为60°,求浮漂B与河堤下端C之间的距离(如图②).
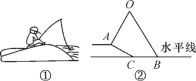
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将等边△ABC绕点C顺时针旋转120°得到△EDC,连接AD,BD.则下列结论:
①AC=AD;②BD⊥AC;③四边形ACED是菱形.
其中正确的个数是( )

A.0 B.1 C.2 D.3
查看答案和解析>>
科目:初中数学 来源: 题型:
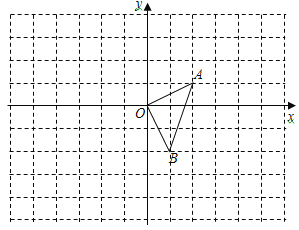
【题目】(8分)如图,在平面直角坐标系中,△OAB的顶点坐标分别为O(0,0)、A(2,1)、B(1,-2).
(1)以原点O为位似中心,在y轴的右侧画出△OAB的一个位似△OA1B1 ,使它与△OAB的相似比为2:1,并分别写出点A、B的对应点A1、B1的坐标.
(2)画出将△OAB向左平移2个单位,再向上平移1个单位后的△O2A2B2 ,并写出点A、B的对应点A2、B2的坐标.
(3)判断△OA1B1与△O2A2B2 ,能否是关于某一点M为位似中心的位似图形,若是,请在图中标出位似中心M,并写出点M的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
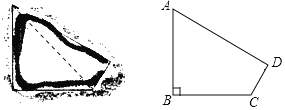
【题目】在海洋上有一近似于四边形的岛屿,其平面如图甲,小明据此构造处该岛的一个数学模型(如图乙四边形ABCD),AC是四边形岛屿上的一条小溪流,其中∠B=90°,AB=BC=5千米,CD=![]() 干米,AD=4
干米,AD=4![]() 干米.
干米.
(1)求小溪流AC的长.
(2)求四边形ABCD的面积.(结果保留根号)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,把一块三角板放在直角坐标系第一象限内,其中30°角的顶点A落在y轴上,直角顶点C落在x轴的(![]() ,0)处,∠ACO=60°,点D为AB边上中点,将△ABC沿x轴向右平移,当点A落在直线y=x﹣3上时,线段CD扫过的面积为_____.
,0)处,∠ACO=60°,点D为AB边上中点,将△ABC沿x轴向右平移,当点A落在直线y=x﹣3上时,线段CD扫过的面积为_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD是⊙O的内接四边形,∠ABC=2∠D,连接OA、OB、OC、AC,OB与AC相交于点E.
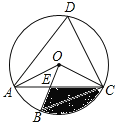
(1)求∠OCA的度数;
(2)若∠COB=3∠AOB,OC=![]() ,求图中阴影部分面积(结果保留π和根号).
,求图中阴影部分面积(结果保留π和根号).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com