
【题目】如图,四边形ABCD是⊙O的内接四边形,∠ABC=2∠D,连接OA、OB、OC、AC,OB与AC相交于点E.
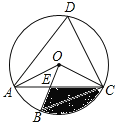
(1)求∠OCA的度数;
(2)若∠COB=3∠AOB,OC=![]() ,求图中阴影部分面积(结果保留π和根号).
,求图中阴影部分面积(结果保留π和根号).
【答案】(1)30°;(2)![]() .
.
【解析】
试题(1)圆内接四边形性质得到∠ABC+∠D=180°,根据∠ABC=2∠D得到∠D+2∠D=180°,从而求得∠D=60°,由OA=OC得到∠OAC=∠OCA=30°;
(2)由∠COB=3∠AOB得到∠AOB=30°,从而有∠COB为直角,然后利用S阴影=S扇形OBC﹣S△OEC求解.
试题解析:(1)∵四边形ABCD是⊙O的内接四边形,∴∠ABC+∠D=180°,∵∠ABC=2∠D,∴∠D+2∠D=180°,∴∠D=60°,∴∠AOC=2∠D=120°,∵OA=OC,∴∠OAC=∠OCA=30°;
(2)∵∠COB=3∠AOB,∴∠AOC=∠AOB+3∠AOB=120°,∴∠AOB=30°,∴∠COB=∠AOC﹣∠AOB=90°,在Rt△OCE中,OC=![]() ,∴OE=OCtan∠OCE=
,∴OE=OCtan∠OCE=![]() tan30°=
tan30°=![]() =2,
=2,
∴S△OEC=![]() OEOC=
OEOC=![]() =
=![]() ,∴S扇形OBC=
,∴S扇形OBC=![]() =3π,∴S阴影=S扇形OBC﹣S△OEC=
=3π,∴S阴影=S扇形OBC﹣S△OEC=![]() .
.


科目:初中数学 来源: 题型:
【题目】甲、乙两位同学在一次用频率估计概率的试验中,统计了某一结果出现的频率,给出的 统计图如图所示,则符合这一结果的试验可能是 ( )
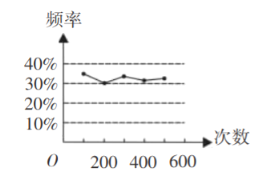
A.掷一枚硬币,出现正面朝上的概率
B.掷一枚硬币,出现反面朝上的概率
C.掷一枚骰子,出现 ![]() 点的概率
点的概率
D.从只有颜色不同的两个红球和一个黄球中,随机取出一个球是黄球的概率
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线y=ax+b与反比例函数y=![]() (x>0)的图像交于A(1,4),B(4,n)两点,与x轴、y轴分别交于C,D两点,则m=________,n=________;若M(x1,y1),N(x2,y2)是反比例函数y=
(x>0)的图像交于A(1,4),B(4,n)两点,与x轴、y轴分别交于C,D两点,则m=________,n=________;若M(x1,y1),N(x2,y2)是反比例函数y=![]() (x>0)的图像上两点,且0<x1<x2,则y1________y2(填“<”“=”或“>”).
(x>0)的图像上两点,且0<x1<x2,则y1________y2(填“<”“=”或“>”).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,AB=AC,∠BAC=100°,将△ABC绕点A顺时针方向旋转40°得到△ADE,BC与AD、DE交于点G、F.
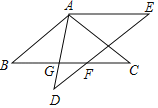
(1)求∠AGC的度数;
(2)求证:四边形ABFE是菱形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,![]() 是
是![]() 的平分线,
的平分线,![]() 是
是![]() 的平分线.
的平分线.
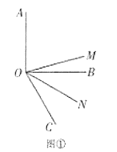
(1)如图①,当![]() 是直角,
是直角,![]() 时,
时,![]() __________,
__________,![]() __________,
__________,![]() __________;
__________;
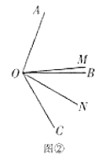
(2)如图②,当![]() ,
,![]() 时,猜想:
时,猜想:![]() 的度数与
的度数与![]() 的数量关系,并说明理由;
的数量关系,并说明理由;
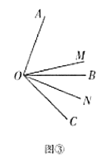
(3)如图③,当![]() ,
,![]() (
(![]() 为锐角)时,猜想:
为锐角)时,猜想:![]() 的度数与
的度数与![]() ,
,![]() 有怎样的数量关系?请写出结论,并说明理由.
有怎样的数量关系?请写出结论,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,⊙O是△ABC的外接圆,![]() =
=![]() ,点D在边BC上,AE∥BC,AE=BD.
,点D在边BC上,AE∥BC,AE=BD.
(1)求证:AD=CE;
(2)如果点G在线段DC上(不与点D重合),且AG=AD,求证:四边形AGCE是平行四边形.

查看答案和解析>>
科目:初中数学 来源: 题型:
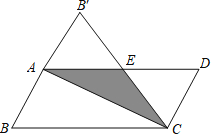
【题目】如图,在平行四边形纸片ABCD中,AB=3cm,将纸片沿对角线AC对折,BC边的对应边B′C与AD边交于点E,此时△CDE恰为等边三角形中,求:
(1)AD的长度.
(2)重叠部分的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】数学课上,老师让学生尺规作图画Rt△ABC,使其斜边AB=c,一条直角边BC=a.李明的作法如图所示,作线段AB使AB=C,以AB为直径作⊙O,以B为圆心,a为半径作弧交⊙O于点C,连接AC,△ABC即为所求作的三角形,你认为这种作法中判断∠ACB是直角的依据是( )
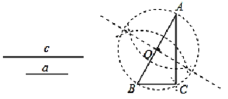
A. 90°的圆周角所对的弦是直径 B. 直径所对的圆周角是直角
C. 勾股定理的逆定理 D. 勾股定理
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明、小华在一栋电梯楼前感慨楼房真高.小明说:“这楼起码20层!”小华却不以为然:“20层?我看没有,数数就知道了!”小明说:“有本事,你不用数也能明白!”小华想了想说:“没问题!让我们来量一量吧!”小明、小华在楼体两侧各选A、B两点,测量数据如图,其中矩形CDEF表示楼体,AB=150米,CD=10米,∠A=30°,∠B=45°,(A、C、D、B四点在同一直线上)问:

(1)楼高多少米?
(2)若每层楼按3米计算,你支持小明还是小华的观点呢?请说明理由.(参考数据:![]() ≈1.73,
≈1.73,![]() ≈1.41,
≈1.41,![]() ≈2.24)
≈2.24)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com