
如图,△AOB≌△ADC,点B和点C是对应顶点,∠O=∠D=90°,记∠OAD=α,∠ABO=β,当BC∥OA时,α与β之间的数量关系为( )

A.α=β B.α=2β C.α+β=90° D.α+2β=180°
B【考点】全等三角形的性质.
【分析】根据全等三角形对应边相等可得AB=AC,全等三角形对应角相等可得∠BAO=∠CAD,然后求出∠BAC=α,再根据等腰三角形两底角相等求出∠ABC,然后根据两直线平行,同旁内角互补表示出∠OBC,整理即可.
【解答】解:∵△AOB≌△ADC,
∴AB=AC,∠BAO=∠CAD,
∴∠BAC=∠O AD=α,
AD=α,
在△ABC中,∠ABC=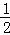 (180°﹣α),
(180°﹣α),
∵BC∥OA,
∴∠OBC=180°﹣∠O=180°﹣90°=90°,
∴β+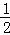 (180°﹣α)=90°,
(180°﹣α)=90°,
整理得,α=2β.
故选B.
【点评】本题考查了全等三角形的性质,等腰三角形两底角相等的性质,平行线的性质,熟记各性质并准确识图理清图中各角度之间的关系是解题的关键.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
已知小丽同学身高1.5米,经太阳光照射,在地面的影长为2米,她此时测得一建筑物在同一地面的影长为40米,那么这个建筑物的高为( )
A.20米 B.30米 C.40米 D.50米
查看答案和解析>>
科目:初中数学 来源: 题型:
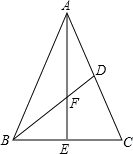
如图,在△ABC中,AB=AC,BD是AC边上的中线,AE⊥BC,垂足为点E,交BD于F,cos∠ABC=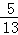 ,AB=13.
,AB=13.
(1)求AE的长;
(2)求tan∠DBC的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com