练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    已知小丽同学身高1.5米，经太阳光照射，在地面的影长为2米，她此时测得一建筑物在同一地面的影长为40米，那么这个建筑物的高为(     )

    A．20米 B．30米 C．40米 D．50米


    B【考点】相似三角形的应用．

    【分析】在同一时刻物高和影长成正比，即在同一时刻的两个物体，影子，经过物体顶部的太阳光线三者构成的两个直角三角形相似．

    【解答】解：根据相同时刻的物高与影长成比例，

    设建筑物的高度为xm，则可列比例为：

    =，

    解得：x=30，

    故选：B．

    【点评】此题主要考查了相似三角形的应用，利用同一时刻物高和影长成正比得出是解题关键．


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：


    如图，△ABC 中，DE 是 AC 的垂直平分线，AE=4cm，△ABD 的周长为 14cm，则△ABC 的周 长为          ．

    查看答案和解析>>

    科目：初中数学 来源： 题型：


     反比例函数的图象如图所示,则K的值可能是

    A.          B.  1          C.  2         D. -1

     


    查看答案和解析>>

    科目：初中数学 来源： 题型：


    已知：如图，D是BC上一点，△ABC∽△ADE，

       求证：∠1＝∠2＝∠3 .

     


    查看答案和解析>>

    科目：初中数学 来源： 题型：


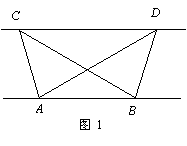
    （1）探究新知：如图1，已知△ABC与△ABD的面积相等，试判断AB与CD的位置

            关系，并说明理由．

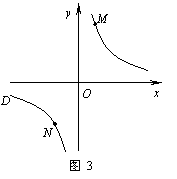
    （2）结论应用：① 如图2，点M，N在反比例函数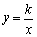（k＞0）的图象上，过点M

    作ME⊥y轴，过点N作NF⊥x轴，垂足分别为E，F．试证明：MN∥EF．   

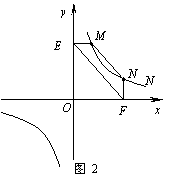
    ② 若①中的其他条件不变，只改变点M，N的位置如图3所示，请判断 MN与

    EF是否平行？请说明理由.

                   

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    已知，AB=4，P是AB黄金分割点，PA＞PB，则PA的长为__________．

    查看答案和解析>>

    科目：初中数学 来源： 题型：


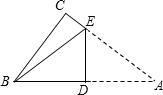
    ．如图，Rt△ABC中，∠C=90°，BC=4，AC=6，现将△ABC沿ED翻折，使点A与点B重合，折痕为DE，则tan∠BED的值是__________．

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    如图，△AOB≌△ADC，点B和点C是对应顶点，∠O=∠D=90°，记∠OAD=α，∠ABO=β，当BC∥OA时，α与β之间的数量关系为（　　）

    A．α=β  B．α=2β C．α+β=90°  D．α+2β=180°

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    如图所示，以平行四边形ABCD的顶点A为圆心，AB为半径作圆，作AD，BC于E，F，延长BA交⊙A于G，判断弧EF和EG是否相等，并说明理由．

    　

    查看答案和解析>>

    同步练习册答案