
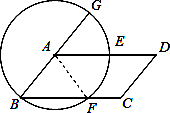
如图所示,以平行四边形ABCD的顶点A为圆心,AB为半径作圆,作AD,BC于E,F,延长BA交⊙A于G,判断弧EF和EG是否相等,并说明理由.
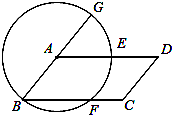
【考点】圆心角、弧、弦的关系;平行四边形的性质.
【分析】要证明 =
=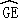 ,则要证明∠DAF=∠GAD,由AB=AF,得出∠ABF=∠AFB,平行四边形的性质得出,AFB=∠DAF,∠GAD=∠ABF,由圆心角、弧、弦的关系定理得出
,则要证明∠DAF=∠GAD,由AB=AF,得出∠ABF=∠AFB,平行四边形的性质得出,AFB=∠DAF,∠GAD=∠ABF,由圆心角、弧、弦的关系定理得出 =
=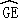 .
.
【解答】解:相等.
理由:连接AF.
∵A为圆心,
∴AB=AF,
∴∠ABF=∠AFB,
∵四边形ABCD为平行四边形,
∴AD∥BC,∠AFB=∠DAF,∠GAD=∠ABF,
∴∠DAF=∠GAD,
∴ =
=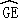 .
.
【点评】本题考查了平行四边形性质,平行线性质,圆心角、弧、弦的关系定理等知识点的应用,关键是求出∠DAF=∠GAD,题目比较典型,难度不大.


科目:初中数学 来源: 题型:
已知小丽同学身高1.5米,经太阳光照射,在地面的影长为2米,她此时测得一建筑物在同一地面的影长为40米,那么这个建筑物的高为( )
A.20米 B.30米 C.40米 D.50米
查看答案和解析>>
科目:初中数学 来源: 题型:
根据下列要求,解答相关问题.
(1)请补全以下求不等式﹣2x2﹣4x>0的解集的过程.
①构造函数,画出图象:根据不等式特征构造二次函数y=﹣2x2﹣4x;并在下面的坐标系中(图1)画出二次函数y=﹣2x2﹣4x的图象(只画出图象即可).
②求得界点,标示所需,当y=0时,求得方程﹣2x2﹣4x=0的解为 ;并用锯齿线标示出函数y=﹣2x2﹣4x图象中y>0的部分.
③借助图象,写出解集:由所标示图象,可得不等式﹣2x2﹣4x>0的解集为﹣2<x<0.请你利用上面求一元一次不等式解集的过程,求不等式x2﹣2x+1≥4的解集.
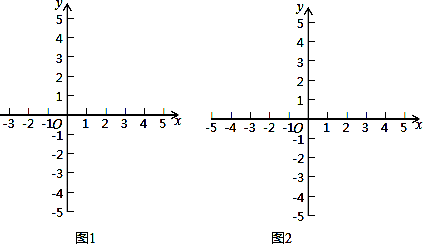
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com