
根据下列要求,解答相关问题.
(1)请补全以下求不等式﹣2x2﹣4x>0的解集的过程.
①构造函数,画出图象:根据不等式特征构造二次函数y=﹣2x2﹣4x;并在下面的坐标系中(图1)画出二次函数y=﹣2x2﹣4x的图象(只画出图象即可).
②求得界点,标示所需,当y=0时,求得方程﹣2x2﹣4x=0的解为 ;并用锯齿线标示出函数y=﹣2x2﹣4x图象中y>0的部分.
③借助图象,写出解集:由所标示图象,可得不等式﹣2x2﹣4x>0的解集为﹣2<x<0.请你利用上面求一元一次不等式解集的过程,求不等式x2﹣2x+1≥4的解集.
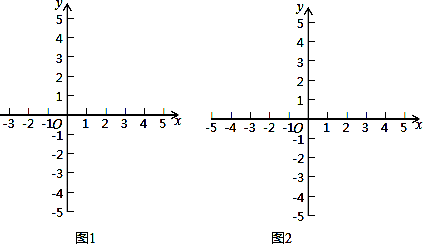
【考点】二次函数与不等式(组).
【分析】①利用描点法即可作出函数的图象;
②当y=0时,解方程求得x的值,当y>0时,就是函数图象在x轴上方的部分,据此即可解得;
③仿照上边的例子,首先作出函数y=x2﹣2x+1的图象,然后求得当y=4时对应的x的值,根据图象即可求解.
【解答】解:①图所示:
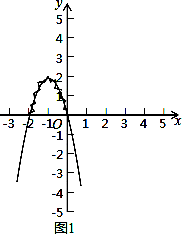 ;
;
②方程﹣2x2﹣4x=0即﹣2x(x+2)=0,
解得:x1=0,x2=﹣2;
则方程的解是x1=0,x2=﹣2,
图象如图1;
③函数y=x2﹣2x+1的图象是:
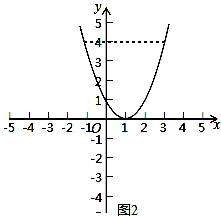
当y=4时,x2﹣2x+1=4,解得:x1=3,x2=﹣1.
则不等式的解集是:x≥3或x≤﹣1.
【点评】本题考查了二次函数与不等式的关系,理解函数的图象在x轴上方,则函数值大于0是本题的关键.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
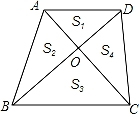
已知:如图,四边形ABCD中,AD∥BC,连接AC,BD交于点O,设△AOD,△AOB,△BOC,△COD的面积分别为S1,S2,S3,S4.
(1)求证:S2=S4;
(2)设AD=m,BC=n,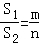 ,
, =
=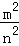 ,根据上述条件,判断S1+S3与S2+S4的大小关系,并说明理由.
,根据上述条件,判断S1+S3与S2+S4的大小关系,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
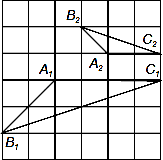
学习相似三角形和解直角三角形的相关内容后,张老师请同学们交流这样的一个问题:“如图,在正方形网格上有△A1B1C1和△A2B2C2,这两个三角形是否相似?”.那么你认为△A1B1C1和△A2B2C2 .(填相似或不相似);理由是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
人体中红细胞的直径约为0.000 007 7 m,用科学记数法表示为
A.7.7×10-5 B.7.7×10-6 C.7.7×10-7 D.77×10-5
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com