
如图,弦AB的长等于⊙O的半径,那么弦AB所对的圆周角的度数是 .
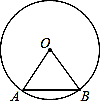
30°或150° .
【考点】圆周角定理;等边三角形的判定与性质.
【分析】首先在优弧上取点C,连接AC,BC,在劣弧AB上取点D,连接AD,BD,由弦AB的长等于⊙O的半径,可得△OAB是等边三角形,然后利用圆周角定理与圆的内接四边形的性质求得答案.
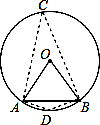
【解答】解:在优弧上取点C,连接AC,BC,在劣弧AB上取点D,连接AD,BD,
∵弦AB的长等于⊙O的半径,
∴△OAB是等边三角形,
∴∠AOB=60°,
∴∠ACB= ∠AOB=30°,
∠AOB=30°,
∴∠ADB=180°﹣∠ACB=150°,
∴弦AB所对的圆周角的度数是:30°或150°.
故答案为:30°或150°.
【点评】此题考查了圆周角定理、圆的内接四边形的性质以及等边三角形的判定与性质.注意准确作出辅助线是解此题的关键.


科目:初中数学 来源: 题型:
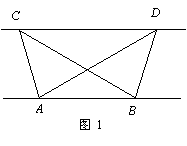
(1)探究新知:如图1,已知△ABC与△ABD的面积相等,试判断AB与CD的位置
关系,并说明理由.
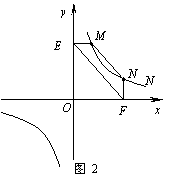
(2)结论应用:① 如图2,点M,N在反比例函数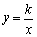 (k>0)的图象上,过点M
(k>0)的图象上,过点M
作ME⊥y轴,过点N作NF⊥x轴,垂足分别为E,F.试证明:MN∥EF.
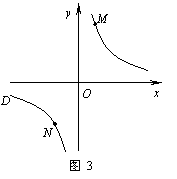
② 若①中的其他条件不变,只改变点M,N的位置如图3所示,请判断 MN与
EF是否平行?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
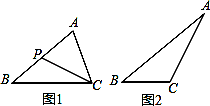
王华在学习相似三角形时,在北京市义务教育教科书九年级上册第31页遇到这样一道题,如图1,在△ABC中,P是边AB上的一点,连接CP,要使△ACP∽△ABC,还需要补充的一个条件是 ,或 .
请回答:
(1)王华补充的条件是 ,或 .
(2)请你参考上面的图形和结论,探究,解答下面的问题:
如图2,在△ABC中,∠A=30°,AC2=AB2+AB•BC.求∠C的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
如图,直线y= -x+3与y轴交于点A,与反比例函数 (k≠0)的图像交于点C,过点C作CB⊥x轴于点B,AO=3BO,
(k≠0)的图像交于点C,过点C作CB⊥x轴于点B,AO=3BO,
则反比例函数的解析式为( )
A.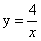 B.
B.
C.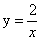 D.
D.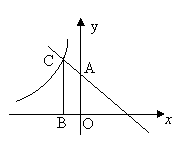
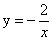
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com