
(1)探究新知:如图1,已知△ABC与△ABD的面积相等,试判断AB与CD的位置
关系,并说明理由.
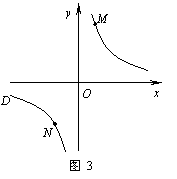
(2)结论应用:① 如图2,点M,N在反比例函数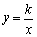 (k>0)的图象上,过点M
(k>0)的图象上,过点M
作ME⊥y轴,过点N作NF⊥x轴,垂足分别为E,F.试证明:MN∥EF.
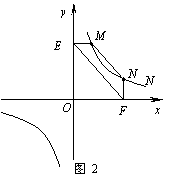
② 若①中的其他条件不变,只改变点M,N的位置如图3所示,请判断 MN与
EF是否平行?请说明理由.
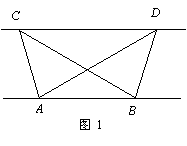
(1)证明:分别过点C,D,作CG⊥AB,DH⊥AB,
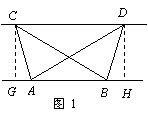 垂足为G,H,则∠CGA=∠DHB=90°.……1分
垂足为G,H,则∠CGA=∠DHB=90°.……1分
∴ CG∥DH.
∵ △ABC与△ABD的面积相等,
∴ CG=DH. …………………………2分
∴ 四边形CGHD为平行四边形.
∴ AB∥CD. ……………………………3分
 (2)①证明:连结MF,NE. …………………4分
(2)①证明:连结MF,NE. …………………4分
设点M的坐标为(x1,y1),点N的坐标为(x2,y2).
∵ 点M,N在反比例函数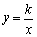 (k>0)的图象上,
(k>0)的图象上,
∴  ,
,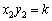 .
.
∵ ME⊥y轴,NF⊥x轴,
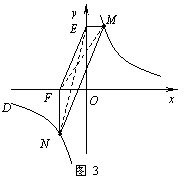 ∴ OE=y1,OF=x2.
∴ OE=y1,OF=x2.
∴ S△EFM=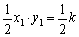 ,
,
S△EFN=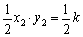 . ………………5分
. ………………5分
∴S△EFM =S△EFN.
由(1)中的结论可知:MN∥EF. ………6分
② MN∥EF. 证明与①类似,略.………7分
(若学生使用其他方法,只要解法正确,皆给分.)


科目:初中数学 来源: 题型:
如图3所示,已知墙的长度是20米,利用墙的一边,用篱笆围成一个面积为96平方米的长方形ABCD,中间用篱笆分隔出两个小长方形,总共用去36米长的篱笆,求AB 的长度?
的长度?
查看答案和解析>>
科目:初中数学 来源: 题型:
如图,正方形OABC,ADEF的顶点A、D、C在坐标轴上,点F在AB 上,点B、E在函数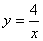 (
(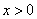 )的图象上,若阴影部分的面积为12 -
)的图象上,若阴影部分的面积为12 -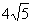 ,则点E的坐标是 .
,则点E的坐标是 .

查看答案和解析>>
科目:初中数学 来源: 题型:
如图,AB是⊙O的直径,CB是弦,OD⊥CB于E,交劣弧CB于D,连接AC.
(1)请写出两个不同的正确结论;
(2)若CB=8,ED=2,求⊙O的半径.
 |
查看答案和解析>>
科目:初中数学 来源: 题型:
已知小丽同学身高1.5米,经太阳光照射,在地面的影长为2米,她此时测得一建筑物在同一地面的影长为40米,那么这个建筑物的高为( )
A.20米 B.30米 C.40米 D.50米
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com