练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

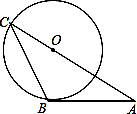
    如图，AB是⊙O的切线，B为切点，AO的延长线交⊙O于C点，连接BC，若∠A=30°，AB=2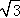，则AC等于（　　）

    A．4       B．6       C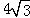． D．

    　


    B【考点】切线的性质．

    【分析】连接OB，则△AOB是直角三角形，利用三角函数即可求得OA的长，则AC即可求解．

    【解答】解：连接OB．

    ∵AB是⊙O的切线，B为切点，

    ∴OB⊥AB，

    在直角△OAB中，OB=AB•tanA=2×=2，

    则OA=2OB=4，

    ∴AC=4+2=6．

    故选B．

    【点评】本题考查了三角函数以及切线的性质，正确判断△OAB是直角三角形是关键．

    　


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：


    已知：如图，D是BC上一点，△ABC∽△ADE，

       求证：∠1＝∠2＝∠3 .

     


    查看答案和解析>>

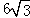
    科目：初中数学 来源： 题型：


    如图，△AOB≌△ADC，点B和点C是对应顶点，∠O=∠D=90°，记∠OAD=α，∠ABO=β，当BC∥OA时，α与β之间的数量关系为（　　）

    A．α=β  B．α=2β C．α+β=90°  D．α+2β=180°

    查看答案和解析>>

    科目：初中数学 来源： 题型：


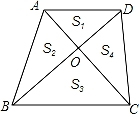
    已知：如图，四边形ABCD中，AD∥BC，连接AC，BD交于点O，设△AOD，△AOB，△BOC，△COD的面积分别为S1，S2，S3，S4．

    （1）求证：S2=S4；

    （2）设AD=m，BC=n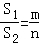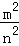，， =，根据上述条件，判断S1+S3与S2+S4的大小关系，并说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    如图，⊙O的半径为5，AB为弦，OC⊥AB，垂足为C，若OC=3，则弦AB的长为（　　）

    A．8       B．6       C．4       D．10

    查看答案和解析>>

    科目：初中数学 来源： 题型：


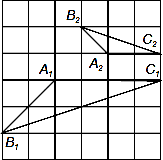
    学习相似三角形和解直角三角形的相关内容后，张老师请同学们交流这样的一个问题：“如图，在正方形网格上有△A1B1C1和△A2B2C2，这两个三角形是否相似？”．那么你认为△A1B1C1和△A2B2C2　　　　　　．（填相似或不相似）；理由是　　　　　　．

    　

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    如图所示，以平行四边形ABCD的顶点A为圆心，AB为半径作圆，作AD，BC于E，F，延长BA交⊙A于G，判断弧EF和EG是否相等，并说明理由．

    　

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    要使是完成平方公式，那么k的值是

      A.                 B.                    C.                 D.

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    为了创建全国卫生城市，某社区要清理一个卫生死角内的垃圾，租用甲、乙两车运送，两车各运12趟可完成，需支付运费4800元．已知甲、乙两车单独运完此堆垃圾，乙车所运趟数是甲车的2倍，且乙车每趟运费比甲车少200元．

    （1）求甲、乙两车单独运完此堆垃圾各需运多少趟？（5分）

    （2）若单独租用一台车，租用哪台车合算？（5分）

    查看答案和解析>>

    同步练习册答案