练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    9．解方程：
    （1）x-2=x（x-2）
    （2）x2-4x-1=0．

    分析 （1）移项后提取公因式后采用因式分解法解一元二次方程即可；
    （2）采用配方法因式分解即可．

    解答 解：（1）移项得：（x-2）-x（x-2）=0，
    提取公因式得：（x-2）（1-x）=0，
    即：x-2=0或1-x=0，
    解得：x=2或x=1；

    （2）移项得：x2-4x=1，
    配方得：x2-4x+4=1+4
    即：（x-2）2=5，
    解得：x-2=$\sqrt{5}$或x-2=-$\sqrt{5}$，
    即：x=2+$\sqrt{5}$或x=2-$\sqrt{5}$．

    点评 本题考查了因式分解法与配方法因式分解的知识，解题的关键是能够根据一元二次方程的不同形式采用合适的方法求解，难度不大，属于基础知识．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：解答题

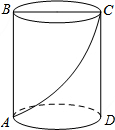    6．如图，一圆柱体的底面周长为24cm，高AB为16cm，BC是上底面的直径．一只昆虫从点A出发，沿着圆柱的侧面爬行到点C，求昆虫爬行的最短路程．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    7．解下列方程：
    （1）$\frac{2x-1}{3}$=$\frac{5x+1}{4}$；
    （2）$\frac{5y}{6}-\frac{y}{3}$=1；
    （3）$\frac{3y+2}{5}$=1-$\frac{y+1}{5}$；
    （4）$\frac{x}{0.3}$-$\frac{x}{0.7}$=1．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    17．下列说法不正确的是（　　）
    A．球的截面一定是圆
    B．组成长方体的各个面中不可能有正方形
    C．从三个不同的方向看正方体，得到的都是正方形
    D．圆锥的截面可能是圆

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    4．计算：
    （1）-20+（-17）-（-18）-11
    （2）23-6×（-3）+2×（-4）
    （3）$-1.53×0.75+0.53×\frac{3}{4}-3.4×0.75$
    （4）$（-24）×（1\frac{3}{8}+2\frac{1}{3}-0.75）$
    （5）$54×\frac{3}{4}-（-54）×\frac{1}{2}+54×（-\frac{1}{4}）$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

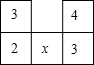    14．如图所示是由几个相同的小正方体所组成的几何体的俯视图，小正方形中的数字表示在该位置的小正方体的个数，请画出这个几何体从正面看和从左面看到的图形，其中x是平方等于本身的正整数．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    1．下列各式中，最简二次根式有（　　）个
    ①$\sqrt{\frac{1}{27}}$；②$\sqrt{{x}^{2}+1}$ ③$\sqrt{o.2}$；④$\sqrt{8}$；⑤$\sqrt{24x}$；⑥$\sqrt{7}$；⑦$\sqrt{3}$；⑧$\sqrt{\frac{27}{8}}$．
    A．1B．2C．3D．4

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    18．下列方程组中，是二元一次方程组的是（　　）
    A．$\left\{\begin{array}{l}{2x-y=7}\\{3y=2x-3}\end{array}\right.$B．$\left\{\begin{array}{l}{x+y=1}\\{xy=12}\end{array}\right.$
    C．$\left\{\begin{array}{l}{\frac{y}{3}-\frac{x}{2}-1}\\{2{x}^{2}+3y-15}\end{array}\right.$D．$\left\{\begin{array}{l}{\frac{1}{x}-\frac{2}{y}=1}\\{x+y=10}\end{array}\right.$

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    19．解方程：
    （1）x+$\frac{x+1}{2}$=1-$\frac{x+2}{3}$
    （2）$\frac{x+1}{0.4}$-$\frac{0.2x-1}{0.7}$=1．

    查看答案和解析>>

    同步练习册答案