
【题目】已知,点B、D分别在∠MAN的两边AM、AN上,点C是射线AP上的一点,连接BC、DC,∠MAN=α,∠BCD=β,(0°<α<180°,0°<β<180°);BE平分∠MBC,DF平分∠NDC.
(1)如图1,若α=β=80°,
①求∠MBC+∠NDC的度数;
②判断BE、DF的位置关系,并说明理由.
(2)如图2,当点C在射线AP上运动时,若直线BE、DF相交于点G,请用含有α、β的代数式表示∠BGD.(直接写结果)
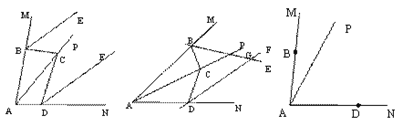
【答案】(1) ① 160°,② 平行;(2)①![]() α-
α- ![]() β,②
β,②![]() β-
β-![]() α,③180°-
α,③180°-![]() α-
α- ![]() β.
β.
【解析】分析: (1) ①利用三角形外角即可求出; ②在①的基础上,再利用角平分线的性质即可求出;
(2)分情况,四边形BCDG是凸四边形,凹四边形来讨论.
详解: (1) ①α=β=80°,
∵∠MBC是△ABC的外角,
∴∠MBC=∠BAC+∠BCA,
同理, ∠NDC=∠DAC+∠ACD,
∴∠MBC+∠NDC=∠BAC+∠BCA+∠DAC+∠ACD
=∠MAN+∠BCD
=α+β
=160°
②BE∥DF
∵BE平分∠MBC, DF平分∠NDC,
∴∠EBC=![]() ∠MBC, ∠CDF=
∠MBC, ∠CDF=![]() ∠NDC,
∠NDC,
∴∠EBC+∠CDF=![]() (∠MBC+∠NDC)=
(∠MBC+∠NDC)= ![]() ×160°=80°,
×160°=80°,
在△BCD中,
∵∠BCD=80°
∴∠CBD+∠CDB=100°
∴∠EBC+∠CBD+∠CDB=180°,
即∠EBD+∠FDB=180°,
∴BE∥DF(同旁内角互补,两直线平行)
(2)①![]() α-
α- ![]() β,②
β,②![]() β-
β-![]() α,③180°-
α,③180°-![]() α-
α- ![]() β.
β.


 课时训练江苏人民出版社系列答案
课时训练江苏人民出版社系列答案 黄冈经典趣味课堂系列答案
黄冈经典趣味课堂系列答案 启东小题作业本系列答案
启东小题作业本系列答案科目:初中数学 来源: 题型:
【题目】如图,点C在以AB为直径的⊙O上,AD与过点C的切线垂直,垂足为点D,AD交⊙O于点E. 
(1)求证:AC平分∠DAB;
(2)连接BE交AC于点F,若cos∠CAD= ![]() ,求
,求 ![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某一工程,在工程招标时,接到甲、乙两个工程队的投标书.甲工程队施工一天,需付工程款1万元;乙工程队施工一天,需付工程款0.6万元.根据甲、乙工程队的投标书测算,可有三种施工方案:
(A)甲队单独完成这项工程,刚好如期完成;
(B)乙队单独完成这项工程要比规定工期多用4天;
(C)若甲、乙两队合做3天后,剩下的工程由乙队单独做,也正好如期完工.
为了节省工程款,同时又能如期完工,你认为应选择哪一种方案?并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】请根据图中提供的信息,回答下列问题

(1)一个暖瓶与一个水杯分别是多少元?
(2)甲、乙两家商场同时出售同样的暖瓶和水杯,为了迎接新年,两家商场都在搞促销活动,甲商场规定: 这两种商品都打九折;乙商场规定:买一个暖瓶赠送一个水杯。若某单位想要买4个暖瓶和15个水杯,请问选择哪家商场购买更合算,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点B、E分别在直线AC和DF上,若∠AGB=∠EHF,∠C=∠D,可以证明∠A=∠F.请完成下面证明过程中的各项“填空”.

证明:∵∠AGB=∠EHF(理由: )
∠AGB= (对顶角相等)
∴∠EHF=∠DGF,∴DB∥EC(理由: )
∴ =∠DBA(两直线平行,同位角相等)
又∵∠C=∠D,∴∠DBA=∠D,
∴DF∥ (内错角相等,两直线平行)
∴∠A=∠F(理由: ).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某装修工程,甲、乙两人可以合作完成,若甲、乙两人合作4天后,再由乙独作12天可以完成,已知甲独作每天需要费用580元.乙独作每天需费用280元.但乙单独完成的天数是甲单独完成天数的2倍.
(1)甲、乙两人单独作这项工程各需多少天?
(2)如果工期要求不超过18天完成,应如何安排甲乙两人的工期使这项工程比较省钱?
查看答案和解析>>
科目:初中数学 来源: 题型:
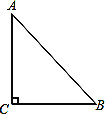
【题目】如果三角形有一边上的中线恰好等于这边的长,那么称这个三角形为“有趣三角形”,这条中线称为“有趣中线”。如图,在三角形ABC中,∠C=90°,较短的一条直角边BC=1,且三角形ABC是“有趣三角形”,求三角形ABC的“有趣中线”的长。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某工厂现有甲种原料3600kg,乙种原料2410kg,计划利用这两种原料生产A,B两种产品共500件,产品每月均能全部售出.已知生产一件A产品需要甲原料9kg和乙原料3kg;生产一件B种产品需甲种原料4kg和乙种原料8kg.
(1)设生产x件A种产品,写出x应满足的不等式组.
(2)问一共有几种符合要求的生产方案?并列举出来.
(3)若有两种销售定价方案,第一种定价方案可使A产品每件获得利润1.15万元,B产品每件获得利润1.25万元;第二种定价方案可使A和B产品每件都获得利润1.2万元;在上述生产方案中哪种定价方案盈利最多?(请用数据说明)
查看答案和解析>>
科目:初中数学 来源: 题型:
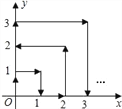
【题目】如图所示一个质点在第一象限内及x轴、y轴上运动,在第一秒内它由原点移动到(0,1)点,而后接着按图所示在x轴,y轴平行的方向运动,且每秒移动一个单位长度,那么质点运动到点(n,n)(n为正整数)的位置时,用代数式表示所用的时间为_________秒.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com