
【题目】已知:平面直角坐标系中,四边形OABC的顶点分别为O(0,0)、A(5,0)、B(m,2)、C(m﹣5,2).
(1)问:是否存在这样的m,使得在边BC上总存在点P,使∠OPA=90°?若存在,求出m的取值范围;若不存在,请说明理由.
(2)当∠AOC与∠OAB的平分线的交点Q在边BC上时,求m的值.
【答案】
(1)
解:存在.
∵O(0,0)、A(5,0)、B(m,2)、C(m﹣5,2).
∴OA=BC=5,BC∥OA,
以OA为直径作⊙D,与直线BC分别交于点E、F,则∠OEA=∠OFA=90°,如图1,
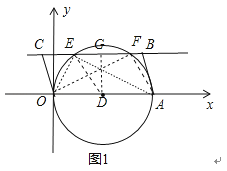
作DG⊥EF于G,连DE,则DE=OD=2.5,DG=2,EG=GF,
∴EG=![]() =1.5,
=1.5,
∴E(1,2),F(4,2),
∴当![]() ,即1≤m≤9时,边BC上总存在这样的点P,使∠OPA=90°
,即1≤m≤9时,边BC上总存在这样的点P,使∠OPA=90°
(2)
解:如图2,

∵BC=OA=5,BC∥OA,
∴四边形OABC是平行四边形,
∴OC∥AB,
∴∠AOC+∠OAB=180°,
∵OQ平分∠AOC,AQ平分∠OAB,
∴∠AOQ=![]() ∠AOC,∠OAQ=
∠AOC,∠OAQ=![]() ∠OAB,
∠OAB,
∴∠AOQ+∠OAQ=90°,
∴∠AQO=90°,
以OA为直径作⊙D,与直线BC分别交于点E、F,则∠OEA=∠OFA=90°,
∴点Q只能是点E或点F,
当Q在F点时,∵OF、AF分别是∠AOC与∠OAB的平分线,BC∥OA,
∴∠CFO=∠FOA=∠FOC,∠BFA=∠FAO=∠FAB,
∴CF=OC,BF=AB,
而OC=AB,
∴CF=BF,即F是BC的中点.
而F点为(4,2),
∴此时m的值为6.5,
当Q在E点时,同理可求得此时m的值为3.5,
综上所述,m的值为3.5或6.5.
【解析】(1)由四边形四个点的坐标易得OA=BC=5,BC∥OA,以OA为直径作⊙D,与直线BC分别交于点E、F,根据圆周角定理得∠OEA=∠OFA=90°,如图1,作DG⊥EF于G,连DE,则DE=OD=2.5,DG=2,根据垂径定理得EG=GF,接着利用勾股定理可计算出EG=1.5,于是得到E(1,2),F(4,2),即点P在E点和F点时,满足条件,此时,即![]() ,即1≤m≤9时,边BC上总存在这样的点P,使∠OPA=90°;
,即1≤m≤9时,边BC上总存在这样的点P,使∠OPA=90°;
(2)如图2,先判断四边形OABC是平行四边形,再利用平行线的性质和角平分线定义可得到∠AQO=90°,以OA为直径作⊙D,与直线BC分别交于点E、F,则∠OEA=∠OFA=90°,于是得到点Q只能是点E或点F,当Q在F点时,证明F是BC的中点.而F点为 (4,2),得到m的值为6.5;当Q在E点时,同理可求得m的值为3.5.


科目:初中数学 来源: 题型:
【题目】甲、乙两人在100米直道AB上练习匀速往返跑,若甲、乙分别中A,B两端同时出发,分别到另一端点处掉头,掉头时间不计,速度分别为5m/s和4m/s.
(1)在坐标系中,虚线表示乙离A端的距离s(单位:m)与运动时间t(单位:s)之间的函数图象(0≤t≤200),请在同一坐标系中用实线画出甲离A端的距离s与运动时间t之间的函数图象(0≤t≤200);
(2)根据(1)中所画图象,完成下列表格:
两人相遇次数 | 1 | 2 | 3 | 4 | … | n |
两人所跑路程之和 | 100 | 300 | … |
|
(3)①直接写出甲、乙两人分别在第一个100m内,s与t的函数解析式,并指出自变量t的取值范围;
②当t=390s时,他们此时相遇吗?若相遇,应是第几次?若不相遇,请通过计算说明理由,并求出此时甲离A端的距离.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD中,∠A=∠ABC=90°,AD=1,BC=3,E是边CD的中点,连接BE并延长与AD的延长线相交于点F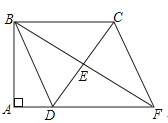
(1)求证:四边形BDFC是平行四边形。
(2)若△BCD是等腰三角形,求四边形BDFC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD中,△ABE经旋转,可与△CBF重合,AE的延长线交FC于点M,以下结论正确的是( ) 
A.AM⊥FC
B.BF⊥CF
C.BE=CE
D.FM=MC
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某片果园有果树80棵,现准备多种一些果树提高果园产量,但是如果多种树,那么树之间的距离和每棵树所受光照就会减少,单棵树的产量随之降低.若该果园每棵果树产果y(千克),增种果树x(棵),它们之间的函数关系如图所示. 
(1)求y与x之间的函数关系式;
(2)在投入成本最低的情况下,增种果树多少棵时,果园可以收获果实6750千克?
(3)当增种果树多少棵时,果园的总产量w(千克)最大?最大产量是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,二次函数y=ax2+bx+c的图象与x轴交于A,B两点,其中点A(﹣1,0),点C(0,5),点D(1,8)都在抛物线上,M为抛物线的顶点. 
(1)求抛物线的函数解析式;
(2)求△MCB的面积;
(3)根据图形直接写出使一次函数值大于二次函数值的x的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com