
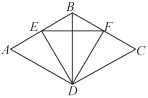
【题目】如图,把等边三角形ABD和等边三角形BCD拼合在一起,点E在AB边上移动,且满足AE=BF,试说明不论点E怎样移动,△EDF总是等边三角形.
科目:初中数学 来源: 题型:
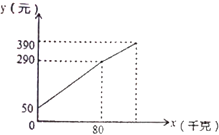
【题目】一水果贩子在批发市场按每千克1.8元批发了若干千克的西瓜进城出售,为了方便,他带了一些零钱备用.他先按市场价售出一些后,又降价出售.售出西瓜千克数![]() 与他手中持有的钱数
与他手中持有的钱数![]() 元(含备用零钱)的关系如图所示,结合图象回答下列问题:
元(含备用零钱)的关系如图所示,结合图象回答下列问题:
(1)农民自带的钱是多少?
(2)降价前他每千克西瓜出售的价格是多少?
(3)随后他按每千克下降0.5元将剩余的西瓜售完,这时他手中的钱(含备用的钱)是390元,问他一共批发了多少千克的西瓜?
(4)请问这个水果贩子一共赚了多少钱?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明同学准备从家打车去南坪,出门后发现到了拥堵使得车辆停滞不前,等了几分钟后他决定步行前往地铁站乘地铁直达南坪站(忽略中途等站和停靠站的时间),在此过程中,他离南坪站的距离y(km)与时间x(h)的函数关系的大致图象是( )
A. 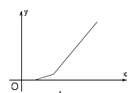 B.
B. 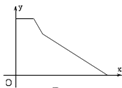
C.  D.
D. 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一次实验中,小明把一根弹簧的上端固定.在其下端悬挂物体,下面是测得的弹簧的长度y与所挂物体质量x的一组对应值.

(1)上表反映了哪两个变量之间的关系?哪个是自变量?哪个是因变量?
(2)当所挂物体重量为3千克时,弹簧多长?不挂重物时呢?
(3)若所挂重物为7千克时(在允许范围内),你能说出此时的弹簧长度吗?
查看答案和解析>>
科目:初中数学 来源: 题型:
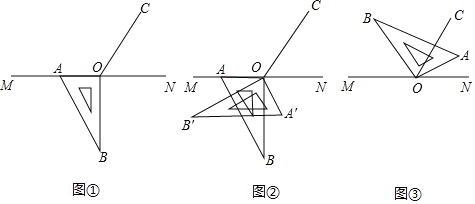
【题目】如图①,点O为直线MN上一点,过点O作直线OC,使∠NOC=60°.将一把直角三角尺的直角顶点放在点O处,一边OA在射线OM上,另一边OB在直线AB的下方,其中∠OBA=30°
(1)将图②中的三角尺沿直线OC翻折至△A′B′O,求∠A′ON的度数;
(2)将图①中的三角尺绕点O按每秒10°的速度沿顺时针方向旋转,旋转角为α(0<α<360°),在旋转的过程中,在第几秒时,直线OA恰好平分锐角∠NOC;
(3)将图①中的三角尺绕点O顺时针旋转,当点A点B均在直线MN上方时(如图③所示),请探究∠MOB与∠AOC之间的数量关系,请直接写出结论,不必写出理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在等腰直角△ABC中∠ABC=90°,AD平分∠BAC,点M、N分别是AD,AB上一动点,当AC=6时,BM+MN的最小值等于_______。

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com