
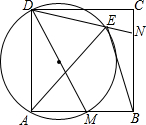
 如图,在正方形ABCD中,M、N分别是AB、BC边上的两个动点,且∠MDN=45°,以DM为直径的圆交DN于点E,连结BE、AE.
如图,在正方形ABCD中,M、N分别是AB、BC边上的两个动点,且∠MDN=45°,以DM为直径的圆交DN于点E,连结BE、AE.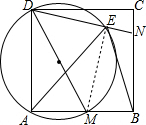
|


 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案 本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案 暑假作业北京艺术与科学电子出版社系列答案
暑假作业北京艺术与科学电子出版社系列答案科目:初中数学 来源: 题型:
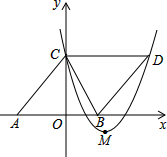 如图,在平面直角坐标系xOy中,菱形ABDC的边AB在x轴上,顶点C在y轴上,A(-6,0),C(0,8),抛物线y=ax2-10ax+c经过点C,且顶点M在直线BC上,则抛物线解析式为
如图,在平面直角坐标系xOy中,菱形ABDC的边AB在x轴上,顶点C在y轴上,A(-6,0),C(0,8),抛物线y=ax2-10ax+c经过点C,且顶点M在直线BC上,则抛物线解析式为查看答案和解析>>
科目:初中数学 来源: 题型:
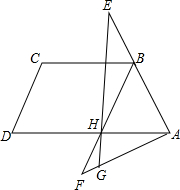 如图,等腰梯形ABCD中,AD∥BC,H是AD中点,AB=BC=CD=
如图,等腰梯形ABCD中,AD∥BC,H是AD中点,AB=BC=CD=| 1 |
| 2 |
查看答案和解析>>
科目:初中数学 来源: 题型:
 某市承办一项大型比赛,在市内有三个体育馆承接所有比赛,现要修建一个运动员公寓,使得运动员公寓到三个体育馆的距离相等,若三个体育馆的位置如图所示,那么运动员公寓应建立在何处?
某市承办一项大型比赛,在市内有三个体育馆承接所有比赛,现要修建一个运动员公寓,使得运动员公寓到三个体育馆的距离相等,若三个体育馆的位置如图所示,那么运动员公寓应建立在何处?查看答案和解析>>
科目:初中数学 来源: 题型:
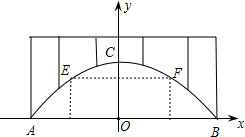 廊桥是我国古老的文化遗产,如图,是某座抛物线型的廊桥示意图,以水面AB所在直线为x轴,AB中点O为原点,建立平面直角坐标系.已知水面AB宽40米,抛物线最高点C到水面AB的距离为10米,为保护廊桥的安全,在该抛物线上距水面AB高为8米的点E,F处要安装两盏警示灯,求这两盏灯的水平距离EF.(结果保留根号)
廊桥是我国古老的文化遗产,如图,是某座抛物线型的廊桥示意图,以水面AB所在直线为x轴,AB中点O为原点,建立平面直角坐标系.已知水面AB宽40米,抛物线最高点C到水面AB的距离为10米,为保护廊桥的安全,在该抛物线上距水面AB高为8米的点E,F处要安装两盏警示灯,求这两盏灯的水平距离EF.(结果保留根号)查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com