
【题目】已知,如图,在ABCD中,延长DA到点E,延长BC到点F,使得AE=CF,连接EF,分别交AB,CD于点M,N,连接DM,BN.
(1)求证:△AEM≌△CFN;
(2)求证:四边形BMDN是平行四边形.
【答案】
(1)
四边形ABCD是平行四边形,
∴∠DAB=∠BCD,
∴∠EAM=∠FCN,
又∵AD∥BC,
∴∠E=∠F.
∵在△AEM与△CFN中,
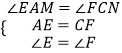 ,
,
∴△AEM≌△CFN(ASA);
(2)
证明:如图
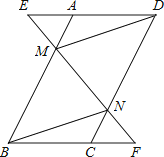
∵四边形ABCD是平行四边形,
∴AB ![]() CD,
CD,
又由(1)得AM=CN,
∴BM ![]() DN,
DN,
∴四边形BMDN是平行四边形.
【解析】(1)先根据平行四边形的性质可得出AD∥BC,∠DAB=∠BCD,再根据平行线的性质及补角的性质得出∠E=∠F,∠EAM=∠FCN,从而利用ASA可作出证明;(2)根据平行四边形的性质及(1)的结论可得BM ![]() DN,则由有一组对边平行且相等的四边形是平行四边形即可证明.
DN,则由有一组对边平行且相等的四边形是平行四边形即可证明.
【考点精析】掌握平行四边形的判定与性质是解答本题的根本,需要知道若一直线过平行四边形两对角线的交点,则这条直线被一组对边截下的线段以对角线的交点为中点,并且这两条直线二等分此平行四边形的面积.


 开心蛙状元测试卷系列答案
开心蛙状元测试卷系列答案科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,定义直线y=ax+b为抛物线y=ax2+bx的特征直线,C(a,b)为其特征点.设抛物线y=ax2+bx与其特征直线交于A、B两点(点A在点B的左侧).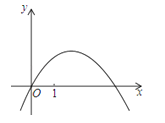
(1)当点A的坐标为(0,0),点B的坐标为(1,3)时,特征点C的坐标为 .
(2)若抛物线y=ax2+bx如图所示,请在所给图中标出点A、点B的位置;
(3)设抛物线y=ax2+bx的对称轴与x轴交于点D,其特征直线交y轴于点E,点F的坐标为(1,0),DE∥CF.
①若特征点C为直线y=﹣4x上一点,求点D及点C的坐标 ;
②若![]() <tan∠ODE<2,则b的取值范围是 .
<tan∠ODE<2,则b的取值范围是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,△ABC的三个顶点坐标分别为A(﹣2,﹣1)、B(﹣1,1)、C(0,﹣2).
(1)点B关于坐标原点O对称的点的坐标为;
(2)将△ABC绕点C顺时针旋转90°,画出旋转后得到的△A1B1C;
(3)求过点B1的反比例函数的解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校为了了解初三年级1000名学生的身体健康情况,从该年级随机抽取了若干名学生,将他们按体重(均为整数,单位:kg)分成五组(A:39.5~46.5;B:46.5~53.5;C:53.5~60.5;D:60.5~67.5;E:67.5~74.5),并依据统计数据绘制了如下两幅尚不完整的统计图.

解答下列问题:
(1)这次抽样调查的样本容量是 ,并补全频数分布直方图;
(2)C组学生的频率为 ,在扇形统计图中D组的圆心角是 度;
(3)请你估计该校初三年级体重超过60kg的学生大约有多少名?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学校为了庆祝校园艺术节,准备购买一批盆花布置校园.已知1盆A种花和2盆B种花一共需13元,2盆A种花和1盆B种花一共需11元.
(1)求1盆A种花和1盒B种花的售价各是多少元?
(2)学校准备购进这两种盆花共100盆,并且A种盆花的数量不超过B种盆花数量的2倍,请求出A种盆花的数量最多是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算
(1)(- 5)+ 6
(2)(+21)+(-31)
(3)(- 5.2 ) + ( - 1.2 )
(4)(﹣3)+7+(﹣6)+(﹣7)
(5)(- 20 ) +(-14)+(-28)+16
(6)5.6+(﹣0.9)+4.4+(﹣8.1)
(7)30 + 15+(-7)+(-15)
(8)![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】老师用![]() 个
个![]() 的小正立方体摆出一个立体图形,它的正视图如图①所示,且图中任两相邻的小正立方体至少有一棱边
的小正立方体摆出一个立体图形,它的正视图如图①所示,且图中任两相邻的小正立方体至少有一棱边![]() 共享,或有一面
共享,或有一面![]() 共享.老师拿出一张
共享.老师拿出一张![]() 的方格纸(如图②),请小荣将此
的方格纸(如图②),请小荣将此![]() 个小正立方体依正视图摆放在方格纸中的方格内,请问小荣摆放完后的左视图有________种.(小正立方体摆放时不得悬空,每一小正立方体的棱边与水平线垂直或平行)
个小正立方体依正视图摆放在方格纸中的方格内,请问小荣摆放完后的左视图有________种.(小正立方体摆放时不得悬空,每一小正立方体的棱边与水平线垂直或平行)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() ABCD中,AD=2AB,F是AD的中点,作
ABCD中,AD=2AB,F是AD的中点,作![]() ,垂足E在线段AB上,连接EF、CF,则下列结论中一定成立的是( )
,垂足E在线段AB上,连接EF、CF,则下列结论中一定成立的是( )

①![]() ②EF=CF
②EF=CF
③![]() ④
④![]()
A. ①②③ B. ①② C. ②③ ④ D. ①②④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,方格纸中的每个小正方形的边长都是1.A、B、C三点都在格点上.
(1)请你以格线所在直线为坐标轴建立平面直角坐标系,使A、B两点的坐标分别为A(﹣2,3),B(﹣3,1),并写出C点坐标;
(2)连接AB、BC、CA得△ABC,将△ABC向右平移4个单位,画出平移后的△A1B1C1;
(3)将△A1B1C1绕点B1按顺时针方向旋转90°,画出旋转后的△A2B1C2 , 并求出在旋转过程中线段A1B1所扫过的图形的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com