
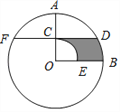
【题目】如图,在⊙O中,半径OA⊥OB,过OA的中点C作FD∥OB交⊙O于D、F两点,且CD=![]() ,以O为圆心,OC为半径作
,以O为圆心,OC为半径作![]() ,交OB于E点.则图中阴影部分的面积为______________.
,交OB于E点.则图中阴影部分的面积为______________.
【答案】![]()
【解析】分析:(1)首先证明OA⊥DF,由垂径定理求出CD=![]() ,由OD=2CO推出∠CDO=30°,设OC=x,则OD=2x,利用勾股定理求得OD的长,再根据S阴=S△CDO+S扇形OBD-S扇形OCE计算即可.
,由OD=2CO推出∠CDO=30°,设OC=x,则OD=2x,利用勾股定理求得OD的长,再根据S阴=S△CDO+S扇形OBD-S扇形OCE计算即可.
详解:连接OD,
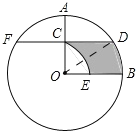
∵OA⊥OB,
∴∠AOB=90°,
∵CD∥OB,
∴∠OCD=90°,
∴OA⊥DF,
∴CD=![]() DF=
DF=![]() ,
,
在Rt△OCD中,∵C是AO中点,
∴OA=OD=2CO,
设OC=x,
则x2+(![]() )2=(2x)2,
)2=(2x)2,
解得:x=1,
∴OA=OD=2,
∵OC=![]() OD,∠OCD=90°,
OD,∠OCD=90°,
∴∠CDO=30°,
∵FD∥OB,
∴∠DOB=∠ODC=30°,
∴S阴=S△CDO+S扇形OBDS扇形OCE=![]() ×1×
×1×![]() +
+![]()
![]() =
=![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】勾股定理是人类最伟大的十个科学发现之一,西方国家称之为毕达哥拉斯定理,但远在毕达哥拉斯出生之前,这一定理早已被人们所利用,世界上各个文明古国都对勾股定理的发现和研究作出过贡献(希腊、中国、埃及、巴比伦、印度等),特别是定理的证明,据说有400余种方法.其中在《几何原本》中有一种证明勾股定理的方法:如图所示,作CG⊥FH,垂足为G,交AB于点P,延长FA交DE于点S,然后将正方形ACED、正方形BCNM作等面积变形,得S正方形ACED=SACQS,S正方形BCNM=SBCQT,这样就可以完成勾股定理的证明.对于该证明过程,下列结论错误的是( )
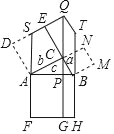
A. △ADS≌△ACB B. SACQS=S矩形APGF
C. SCBTQ=S矩形PBHG D. SE=BC
查看答案和解析>>
科目:初中数学 来源: 题型:
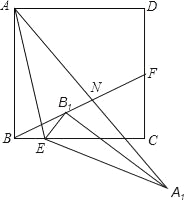
【题目】如图,正方形ABCD中,AB=4,点E是BC上一点,且tan∠BAE=![]() ,点F是CD的中点,连接AE、BF将△ABE着点E按顺时针方向旋转,使点B落在BF上的B1处位置处,点A经过旋转落在A1点位置处,连接AA1交BF于点N.
,点F是CD的中点,连接AE、BF将△ABE着点E按顺时针方向旋转,使点B落在BF上的B1处位置处,点A经过旋转落在A1点位置处,连接AA1交BF于点N.
(1)求证:∠BFC=∠A1 B1F;
(2)说明点N是AA1的中点;
(3)求AN的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】从边长为a的正方形中剪掉一个边长为b的正方形(如图1),然后将剩余部分拼成一个长方形(如图2).
(1)探究:上述操作能验证的等式是 ;(请选择正确的一个)

A.a2-2ab+b2=(a-b)2 B.a2-b2=(a+b)(a-b)
C.a2+ab=a(a+b)
(2)应用:利用你从(1)选出的等式,完成下列各题:
①已知9x2-4y2=24,3x+2y=6,求3x-2y的值;
②计算:![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB为直径,AB=4,C、D为圆上两个动点,N为CD中点,CM⊥AB于M,当C、D在圆上运动时保持∠CMN=30°,则CD的长( )
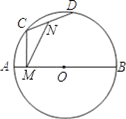
A. 随C、D的运动位置而变化,且最大值为4 B. 随C、D的运动位置而变化,且最小值为2
C. 随C、D的运动位置长度保持不变,等于2 D. 随C、D的运动位置而变化,没有最值
查看答案和解析>>
科目:初中数学 来源: 题型:
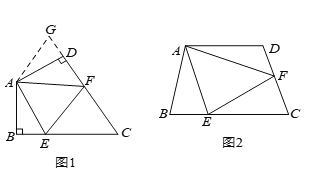
【题目】如图(![]() ),在四边形
),在四边形![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 分别是
分别是![]() ,
,![]() 上的点,且
上的点,且![]() .探究图中线段
.探究图中线段![]() ,
,![]() ,
,![]() 之间的数量关系.小王同学探究此问题的方法是,延长
之间的数量关系.小王同学探究此问题的方法是,延长![]() 到点
到点![]() ,使
,使![]() ,连接
,连接![]() ,先证明
,先证明![]() ≌
≌![]() ,再证明
,再证明![]() ≌
≌![]() ,可得出结论,他的结论应该是__________.
,可得出结论,他的结论应该是__________.
如图(![]() ),若在四边形
),若在四边形![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() 分别是
分别是![]() ,
,![]() 上的点,且
上的点,且![]() ,上述结论是否仍然成立,并说明理由.
,上述结论是否仍然成立,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
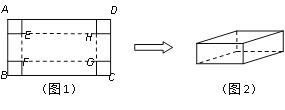
【题目】在一张足够大的纸板上截取一个面积为3600平方厘米的矩形纸板ABCD,如图1,再在矩形纸板的四个角上切去边长相等的小正方形,再把它的边沿虚线折起,做成一个无盖的长方体纸盒,底面为矩形EFGH,如图2.设小正方形的边长为x厘米.
(1)当矩形纸板ABCD的一边长为90厘米时,求纸盒的侧面积的最大值;
(2)当EH:EF=7:2,且侧面积与底面积之比为9:7时,求x的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲骑自行年,乙乘坐汽车从A地出发沿同一路线匀速前往B地,甲先出发.设甲行驶的时间为x(h),甲、乙两人距出发点的路程S甲(km)、S乙(km)关于x的函数图象如图1所示,甲、乙两人之同的距离y(km)关于x的函数图象如图2所示,请你解决以下问题:
(1)甲的速度是__________km/h,乙的速度是_______km/h;
(2)a=_______,b=_______;
(3)甲出发多少时间后,甲、乙两人第二次相距7.5km?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC中,∠B=90°,AB=16cm,BC=12cm,P、Q是△ABC边上的两个动点,其中点P从点A开始沿A→B方向运动,且速度为每秒1cm,点Q从点B开始沿B→C→A方向运动,且速度为每秒2cm,它们同时出发,设出发的时间为t秒.
(1)出发2秒后,求PQ的长.
(2)当点Q在边BC上运动时,出发几秒钟后,△PQB能形成等腰三角形?
(3)当点Q在边CA上运动时,求能使△BCQ成为等腰三角形的运动时间.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com