
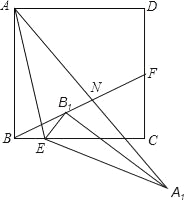
【题目】如图,正方形ABCD中,AB=4,点E是BC上一点,且tan∠BAE=![]() ,点F是CD的中点,连接AE、BF将△ABE着点E按顺时针方向旋转,使点B落在BF上的B1处位置处,点A经过旋转落在A1点位置处,连接AA1交BF于点N.
,点F是CD的中点,连接AE、BF将△ABE着点E按顺时针方向旋转,使点B落在BF上的B1处位置处,点A经过旋转落在A1点位置处,连接AA1交BF于点N.
(1)求证:∠BFC=∠A1 B1F;
(2)说明点N是AA1的中点;
(3)求AN的长.
【答案】(1)详见解析; (2)详见解析;(3)![]() .
.
【解析】试题分析:(1)已知四边形ABCD是正方形,根据正方形的性质可得AB∥CD,即可得∠ABF=∠CFB,由旋转的性质可得EB=EB1,根据等腰三角形的性质可得∠EBB1=∠EB1B,再由∠ABC=∠EB1A1=90°,即可得∠ABF+∠EBB′=90°,∠BB1E+∠A1B1F=90°,所以∠A1B1F=∠ABF=∠BFC;(2)作EP⊥BF,A1Q⊥BF,取BC的中点M,连接AB1,B1M,可得点P是BB1的中点,根据三角形的中位线定理可得EP∥MB1,即可得MB1⊥BB1;易证△BPE∽△BCF,即可求得BP=![]() ,EP=
,EP=![]() ,从而求得BB1=
,从而求得BB1=![]() ,再证明A,B1,M三点共线,即可得AB1=
,再证明A,B1,M三点共线,即可得AB1=![]() ,再证明△AB1N≌△A1QN,即可得AN=A1N,从而证得N是AA1的中点;(3)由△AB1N≌△A1QN,可得B1N=
,再证明△AB1N≌△A1QN,即可得AN=A1N,从而证得N是AA1的中点;(3)由△AB1N≌△A1QN,可得B1N=![]() B1Q=
B1Q=![]() ,根据勾股定理即可求得AN=
,根据勾股定理即可求得AN=![]() .
.
试题解析:
(1)∵四边形ABCD是正方形,
∴AB∥CD,
∴∠ABF=∠CFB,
∵EB=EB1,
∴∠EBB1=∠EB1B,
∵∠ABC=∠EB1A1=90°,
∴∠ABF+∠EBB′=90°,∠BB1E+∠A1B1F=90°,
∴∠A1B1F=∠ABF=∠BFC.
(2)作EP⊥BF,A1Q⊥BF,取BC的中点M,连接AB1,B1M,
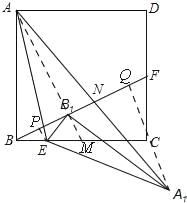
∴点P是BB1的中点,
∵E是BM中点,
∴EP∥MB1,
∴MB1⊥BB1,
由旋转得,△BPE∽△BCF,
∴BP=![]() ,EP=
,EP=![]() ,
,
∵PB1=PB=![]() ,
,
∴BB1=![]() ,
,
∵sin∠FBC=![]() =
=![]() =
=![]() ,
,
∴∠AB1B=90°,
∴A,B1,M三点共线,
∴AB1=![]() ,
,
∵∠B1A1Q=∠BB1E=∠FBC,
∴△B1QA1∽△FCB,
∴B1Q=![]() ,A1Q=
,A1Q=![]() =AB1,
=AB1,
∴△AB1N≌△A1QN,
∴AN=A1N,
∴N是AA1的中点.
(3)∵△AB1N≌△A1QN,
∴B1N=![]() B1Q=
B1Q=![]() ,
,
根据勾股定理得,AN=![]() =
=![]() .
.


科目:初中数学 来源: 题型:
【题目】已知把直线y=kx+b(k≠0)沿着y轴向上平移3个单位后,得到直线y=﹣2x+5.
(1)求直线y=kx+b(k≠0)的解析式;
(2)求直线y=kx+b(k≠0)与坐标轴围成的三角形的周长.
查看答案和解析>>
科目:初中数学 来源: 题型:
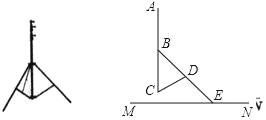
【题目】某数码产品专卖店的一块摄像机支架如图所示,将该支架打开立于地面MN上,主杆AC与地面垂直,调节支架使得脚架BE与主杆AC的夹角∠CBE=45°,这时支架CD与主杆AC的夹角∠BCD恰好等于60°,若主杆最高点A到调节旋钮B的距离为40cm.支架CD的长度为30cm,旋转钮D是脚架BE的中点,求脚架BE的长度和支架最高点A到地面的距离.(结果保留根号)
查看答案和解析>>
科目:初中数学 来源: 题型:
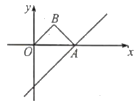
【题目】如图,直线y=x﹣4与x轴交于点A,以OA为斜边在x轴上方作等腰Rt△OAB,并将Rt△AOB沿x轴向右平移,当点B落在直线y=x﹣4上时,Rt△OAB扫过的面积是__.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】用同样大小的黑色棋子按如图所示的规律摆放:

(1)分别写出第6、7两个图形各有多少颗黑色棋子?
(2)写出第n个图形黑色棋子的颗数?
(3)是否存在某个图形有1020颗黑色棋子?若存在,求出是第几个图形;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平行四边形ABCD中,∠C=120°,AD=2AB=4,点H、G分别是边CD、BC上的动点.连接AH、HG,点E为AH的中点,点F为GH的中点,连接EF.则EF的最大值与最小值的差为( )

A. 1 B. ![]() ﹣1 C.
﹣1 C. ![]() D. 2﹣
D. 2﹣![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
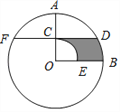
【题目】如图,在⊙O中,半径OA⊥OB,过OA的中点C作FD∥OB交⊙O于D、F两点,且CD=![]() ,以O为圆心,OC为半径作
,以O为圆心,OC为半径作![]() ,交OB于E点.则图中阴影部分的面积为______________.
,交OB于E点.则图中阴影部分的面积为______________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】观察下面的点阵图和相应的等式,探究其中的规律:
(1)在④后面的横线上写出相应的等式:

①1=12;②1+3=22;③1+3+5=32;④ ;⑤1+3+5+7+9=52;…
(2)请写出第n个等式;
(3)利用(2)中的等式,计算21+23+25+…+99.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com