
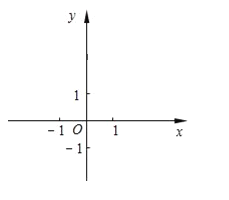
【题目】已知把直线y=kx+b(k≠0)沿着y轴向上平移3个单位后,得到直线y=﹣2x+5.
(1)求直线y=kx+b(k≠0)的解析式;
(2)求直线y=kx+b(k≠0)与坐标轴围成的三角形的周长.
 桃李文化快乐暑假武汉出版社系列答案
桃李文化快乐暑假武汉出版社系列答案 优秀生快乐假期每一天全新寒假作业本系列答案
优秀生快乐假期每一天全新寒假作业本系列答案 暑假接力赛新疆青少年出版社系列答案
暑假接力赛新疆青少年出版社系列答案科目:初中数学 来源: 题型:
【题目】2017年元旦期间,某商场打出促销广告,如表所示.
优惠 条件 | 一次性购物不超过200元 | 一次性购物超过200元,但不超过500元 | 一次性购物超过500元 |
优惠 办法 | 没有优惠 | 全部按九折优惠 | 其中500元仍按九折优惠,超过500元部分按八折优惠 |
小欣妈妈两次购物分别用了134元和490元.
(1)小欣妈妈这两次购物时,所购物品的原价分别为多少?
(2)若小欣妈妈将两次购买的物品一次全部买清,则她是更节省还是更浪费?说说你的理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】电子跳蚤游戏盘是如图所示的△ABC,AB=AC=BC=5.如果跳蚤开始时在BC边的P0处,BP0=2.跳蚤第一步从P0跳到AC边的P1(第1次落点)处,且CP1= CP0;第二步从P1跳到AB边的P2(第2次落点)处,且AP2= AP1;第三步从P2跳到BC边的P3(第3次落点)处,且BP3= BP2;…;跳蚤按照上述规则一直跳下去,第n次落点为Pn(n为正整数),则点P2016与点P2017之间的距离为_________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在直角坐标系中点![]() 的坐标为(1,0),过点
的坐标为(1,0),过点![]() 作x轴的垂线交直线y=2x于
作x轴的垂线交直线y=2x于![]() ,过点
,过点![]() 作直线y=2x的垂线交x轴于
作直线y=2x的垂线交x轴于![]() ,过点
,过点![]() 作x轴的垂线交直线y=2x于
作x轴的垂线交直线y=2x于![]() …,依此规律,则
…,依此规律,则![]() 的坐标为___________.
的坐标为___________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,长方形纸片ABCD中,AB=6 cm,BC=8 cm,点E是BC边上一点,连接AE,并将△AEB沿AE折叠,得到△AEB′,以C,E,B′为顶点的三角形是直角三角形时,BE的长为____cm.

查看答案和解析>>
科目:初中数学 来源: 题型:
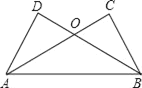
【题目】如图,AC⊥BC,AD⊥DB,下列条件中: ①∠ABD=∠BAC;②∠DAB=∠CBA;③AD=BC;④∠DAC=∠CBD,能使△ABC≌△BAD的有_____(把所有正确结论的序号都填在横线上)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】勾股定理是人类最伟大的十个科学发现之一,西方国家称之为毕达哥拉斯定理,但远在毕达哥拉斯出生之前,这一定理早已被人们所利用,世界上各个文明古国都对勾股定理的发现和研究作出过贡献(希腊、中国、埃及、巴比伦、印度等),特别是定理的证明,据说有400余种方法.其中在《几何原本》中有一种证明勾股定理的方法:如图所示,作CG⊥FH,垂足为G,交AB于点P,延长FA交DE于点S,然后将正方形ACED、正方形BCNM作等面积变形,得S正方形ACED=SACQS,S正方形BCNM=SBCQT,这样就可以完成勾股定理的证明.对于该证明过程,下列结论错误的是( )
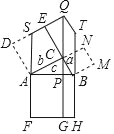
A. △ADS≌△ACB B. SACQS=S矩形APGF
C. SCBTQ=S矩形PBHG D. SE=BC
查看答案和解析>>
科目:初中数学 来源: 题型:
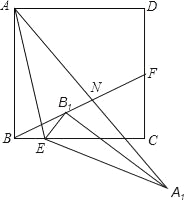
【题目】如图,正方形ABCD中,AB=4,点E是BC上一点,且tan∠BAE=![]() ,点F是CD的中点,连接AE、BF将△ABE着点E按顺时针方向旋转,使点B落在BF上的B1处位置处,点A经过旋转落在A1点位置处,连接AA1交BF于点N.
,点F是CD的中点,连接AE、BF将△ABE着点E按顺时针方向旋转,使点B落在BF上的B1处位置处,点A经过旋转落在A1点位置处,连接AA1交BF于点N.
(1)求证:∠BFC=∠A1 B1F;
(2)说明点N是AA1的中点;
(3)求AN的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com