
【题目】如图,一次函数y=-2x+2的图象与![]() 轴、
轴、![]() 轴分别交于点
轴分别交于点![]() 、
、![]() ,以线段
,以线段![]() 为直角边在第一象限内作等腰直角三角形ABC,且
为直角边在第一象限内作等腰直角三角形ABC,且![]() ,则点C坐标为_____.
,则点C坐标为_____.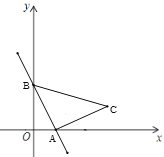
 心算口算巧算一课一练系列答案
心算口算巧算一课一练系列答案 应用题作业本系列答案
应用题作业本系列答案科目:初中数学 来源: 题型:
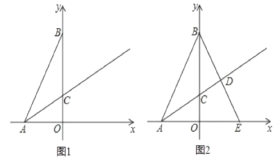
【题目】已知O为直线AB上的一点,COE是直角,OF平分AOE(图中所说的角都是小于平角的角).
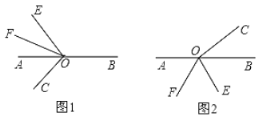
(1)如图1,若COF58°,求BOE的度数;
(2)将COE绕点O顺时针旋转到如图2所示的位置时,若COFm°,求BOE的度数(用含字母m的代数式表示).
查看答案和解析>>
科目:初中数学 来源: 题型:
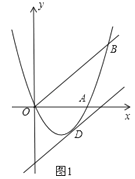
【题目】如图1,已知抛物线y=ax2+bx(a≠0)经过A(6,0)、B(8,8)两点.
(1)求抛物线的解析式;
(2)将直线OB向下平移m个单位长度后,得到的直线与抛物线只有一个公共点D,求m的值及点D的坐标;
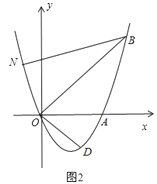
(3)如图2,若点N在抛物线上,且∠NBO=∠ABO,则在(2)的条件下,在坐标平面内有点P,求出所有满足△POD∽△NOB的点P坐标(点P、O、D分别与点N、O、B对应).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知把直线y=kx+b(k≠0)沿着y轴向上平移3个单位后,得到直线y=﹣2x+5.
(1)求直线y=kx+b(k≠0)的解析式;
(2)求直线y=kx+b(k≠0)与坐标轴围成的三角形的周长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】观察算式:1×3+1=4=22;2×4+1=9=32;3×5+1=16=42;4×6+1=25=52,…
(1)请根据你发现的规律填空:6×8+1=( )2;
(2)用含n的等式表示上面的规律: ;
(3)用找到的规律解决下面的问题:
计算:(1+![]() )(1+
)(1+![]() )(1+
)(1+![]() )(1+
)(1+![]() )…(1+
)…(1+![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,平面直角坐标系中,点A(6![]() ,0),点B(0,18),∠BAO=60°,射线AC平分∠BAO交y轴正半轴于点C.
,0),点B(0,18),∠BAO=60°,射线AC平分∠BAO交y轴正半轴于点C.
(1)求点C的坐标;
(2)点N从点A以每秒2个单位的速度沿线段AC向终点C运动,过点N作x轴的垂线,分别交线段AB于点M,交线段AO于点P,设线段MP的长度为d,点P的运动时间为t,请求出d与t的函数关系式(直接写出自变量t的取值范围);
(3)在(2)的条件下,将△ABO沿y轴翻折,点A落在x轴正半轴上的点E,线段BE交射线AC于点D,点Q为线段OB上的动点,当△AMN与△OQD全等时,求出t值并直接写出此时点Q的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
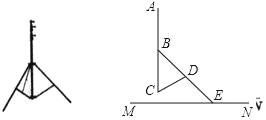
【题目】某数码产品专卖店的一块摄像机支架如图所示,将该支架打开立于地面MN上,主杆AC与地面垂直,调节支架使得脚架BE与主杆AC的夹角∠CBE=45°,这时支架CD与主杆AC的夹角∠BCD恰好等于60°,若主杆最高点A到调节旋钮B的距离为40cm.支架CD的长度为30cm,旋转钮D是脚架BE的中点,求脚架BE的长度和支架最高点A到地面的距离.(结果保留根号)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com