
【题目】已知O为直线AB上的一点,COE是直角,OF平分AOE(图中所说的角都是小于平角的角).
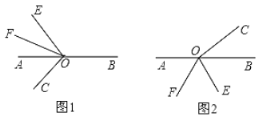
(1)如图1,若COF58°,求BOE的度数;
(2)将COE绕点O顺时针旋转到如图2所示的位置时,若COFm°,求BOE的度数(用含字母m的代数式表示).
【答案】(1)116°;(2)360°﹣2m°.
【解析】
(1)根据互余得到∠EOF的度数,再由OF平分∠AOE,得到∠AOE=2∠EOF,然后根据邻补角的定义得到∠BOE的度数;
(2)当∠COF=m°,根据互余得到∠EOF=m°﹣90°,再由OF平分∠AOE,得到∠AOE=2∠EOF=2m°﹣180°,然后根据邻补角的定义得到∠BOE的度数,即可得到结论.
(1)∵∠COE是直角,∠COF=58°,∴∠EOF=90°﹣58°=32°.
∵OF平分∠AOE,∴∠AOE=2∠EOF=64°,∴∠BOE=180°﹣64°=116°.
故答案为:116°;
(2)∵∠COF=m°,∴∠EOF=m°﹣90°.
又∵OF平分∠AOE,∴∠AOE=2∠EOF=2m°﹣180°,∴∠BOE=180°﹣(2m°﹣180°)=360°﹣2m°.


科目:初中数学 来源: 题型:
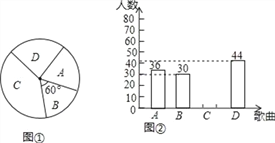
【题目】为庆祝建军90周年,某校计划在五月份举行“唱响军歌”歌咏比赛,要确定一首喜欢人数最多的歌曲为每班必唱歌曲.为此提供代号为A,B,C,D四首备选曲目让学生选择,经过抽样调查,并将采集的数据绘制如下两幅不完整的统计图.请根据图①,图②所提供的信息,
解答下列问题:
(1)本次抽样调查中,选择曲目代号为A的学生占抽样总数的百分比为 ;
(2)请将图②补充完整;
(3)若该校共有1260名学生,根据抽样调查的结果估计全校共有多少学生选择喜欢人数最多的歌曲?(要有解答过程)
查看答案和解析>>
科目:初中数学 来源: 题型:
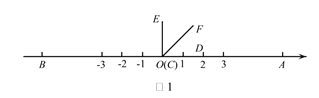
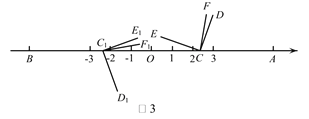
【题目】如图1,在数轴上A,B两点对应的数分别是6,-6, ![]() (C与O重合,D点在数轴的正半轴上)
(C与O重合,D点在数轴的正半轴上)
(1)如图1,若CF 平分![]() ,则
,则![]() _________;
_________;
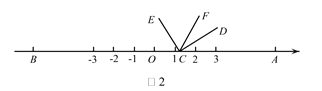
(2)如图2,将![]() 沿数轴的正半轴向右平移t(0<t<3)个单位后,再绕点顶点
沿数轴的正半轴向右平移t(0<t<3)个单位后,再绕点顶点![]() 逆时针旋转30t度,作
逆时针旋转30t度,作![]() 平分
平分![]() ,此时记
,此时记![]() .
.
①当t=1时, ![]() _______;
_______;
②猜想![]() 和
和![]() 的数量关系,并证明;
的数量关系,并证明;
(3)如图3,开始![]() 与
与![]() 重合,将
重合,将![]() 沿数轴的正半轴向右平移t(0<t<3)个单位,再绕点顶点
沿数轴的正半轴向右平移t(0<t<3)个单位,再绕点顶点![]() 逆时针旋转30t度,作
逆时针旋转30t度,作![]() 平分
平分![]() ,此时记
,此时记![]() ,与此同时,将
,与此同时,将![]() 沿数轴的负半轴向左平移t(0<t<3)个单位,再绕点顶点
沿数轴的负半轴向左平移t(0<t<3)个单位,再绕点顶点![]() 顺时针旋转30t度,作
顺时针旋转30t度,作![]() 平分
平分![]() ,记
,记![]() ,若
,若![]() 与
与![]() 满足
满足![]() ,请直接写出t的值为_________.
,请直接写出t的值为_________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2017年元旦期间,某商场打出促销广告,如表所示.
优惠 条件 | 一次性购物不超过200元 | 一次性购物超过200元,但不超过500元 | 一次性购物超过500元 |
优惠 办法 | 没有优惠 | 全部按九折优惠 | 其中500元仍按九折优惠,超过500元部分按八折优惠 |
小欣妈妈两次购物分别用了134元和490元.
(1)小欣妈妈这两次购物时,所购物品的原价分别为多少?
(2)若小欣妈妈将两次购买的物品一次全部买清,则她是更节省还是更浪费?说说你的理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示.点C,B 是线段 AD 上的两点, AC : CB : BD 3 :1: 4 ,点 E , F 分别是 AB,CD 的中点,且 EF 14 ,求 AB,CD 的长.
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在ABCD中,∠DAB的平分线交CD于点E,交BC的延长线于点G,∠ABC的平分线交CD于点F,交AD的延长线于点H,AG与BH交于点O,连接BE,下列结论错误的是( )
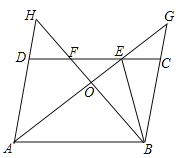
A. BO=OH B. DF=CE C. DH=CG D. AB=AE
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,OA⊥OB,AB⊥x轴于点C,点A(![]() ,1)在反比例函数
,1)在反比例函数![]() 的图象上.
的图象上.

(1)求反比例函数![]() 的表达式;
的表达式;
(2)在x轴的负半轴上存在一点P,使得S△AOP=![]() S△AOB,求点P的坐标;
S△AOB,求点P的坐标;
(3)若将△BOA绕点B按逆时针方向旋转60°得到△BDE.直接写出点E的坐标,并判断点E是否在该反比例函数的图象上,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】电子跳蚤游戏盘是如图所示的△ABC,AB=AC=BC=5.如果跳蚤开始时在BC边的P0处,BP0=2.跳蚤第一步从P0跳到AC边的P1(第1次落点)处,且CP1= CP0;第二步从P1跳到AB边的P2(第2次落点)处,且AP2= AP1;第三步从P2跳到BC边的P3(第3次落点)处,且BP3= BP2;…;跳蚤按照上述规则一直跳下去,第n次落点为Pn(n为正整数),则点P2016与点P2017之间的距离为_________.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com