练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】如图所示.点C，B 是线段 AD 上的两点， AC : CB : BD 3 :1: 4 ，点 E ， F 分别是 AB，CD 的中点，且 EF 14 ，求 AB，CD 的长.

    【答案】AB=16，CD=20．

    【解析】

    根据已知条件“AC：CB：BD=3：1：4”设AC=3x，则CB=x，BD=4x，表示出BE，CF，根据EF=14列方程求解，即可得到x的值．从而求得线段AB、CD的长．

    设AC=3x，则CB=x，BD=4x，∴AB=AC+CB=3x+x=4x，CD=CB+BD=x+4x=5x．

    ∵点E，F分别是AB，CD的中点则BE=AB=2x，CF=CD=．

    ∵EF=14，∴EB+CF-CB=14，∴=14，解得：x=4，

    ∴AB=4x=16，CD=5x=20．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】某校学生利用双休时间去距学校10 km的天平山社会实践活动，一部分学生骑电瓶车先走，过了20 min后，其余学生乘公交车沿相同路线出发，结果他们同时到达．已知公交车的速度是电瓶车学生速度的2倍，求骑电瓶车学生的速度和公交车的速度？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某水果批发市场规定，一次购买苹果不超过100kg（包括100kg），批发价为5元，如果一次购买100kg以上苹果，超过100kg的部分苹果价格打8折．

    （I）请填写下表

    购买量/kg

    0

    50

    100

    150

    200

    …

    付款金额/元

    0

    250

    _

    700

    __

    …

    （Ⅱ）写出付款金额关于购买量的函数解析式；

    （Ⅲ）如果某人付款2100元，求其购买苹果的数量．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】在平面直角坐标系中，已知点A(0，－2)、B(0，3)，点C是x轴正半轴上的一点，当∠BCA＝45°时，点C的坐标为__________________；

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，直线EF与MN相交于点O，∠MOE=30°，将一直角三角尺的直角顶点与点O重合，直角边OA与MN重合，OB在∠NOE内部．操作：将三角尺绕点O以每秒5°的速度沿顺时针方向旋转一周，设运动时间为t（s）．

    (1)当t为何值时，直角边OB恰好平分∠NOE？此时OA是否平分∠MOE？请说明理由；

    (2)若在三角尺转动的同时，直线EF也绕点O以每秒8°的速度顺时针方向旋转一周，当一方先完成旋转一周时，另一方同时停止转动．

    ①当t为何值时，OE平分∠AOB？

    ②OE能否平分∠NOB？若能请直接写出t的值；若不能，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知O为直线AB上的一点，COE是直角，OF平分AOE（图中所说的角都是小于平角的角）.

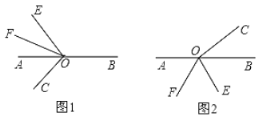
    （1）如图1，若COF58°，求BOE的度数；

    （2）将COE绕点O顺时针旋转到如图2所示的位置时，若COFm°，求BOE的度数（用含字母m的代数式表示）.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，从直径为2cm的圆形纸片中，剪出一个圆心角为90°的扇形OAB，且点O、A、B在圆周上，把它围成一个圆锥，则圆锥的底面圆的半径是 cm．

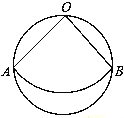
    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，E是ABCD的边CD的中点，延长AE交BC的延长线于点F．

    （1）求证：△ADE≌△FCE．

    （2）若∠BAF=90°，BC=5，EF=3，求CD的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】观察算式：1×3+1＝4＝22；2×4+1＝9＝32；3×5+1＝16＝42；4×6+1＝25＝52，…

    （1）请根据你发现的规律填空：6×8+1＝（　 　）2；

    （2）用含n的等式表示上面的规律：　 　；

    （3）用找到的规律解决下面的问题：

    计算：（1+）（1+）（1+）（1+）…（1+）

    查看答案和解析>>

    同步练习册答案