
ΓΨΧβΡΩΓΩ»γΆΦ1Θ§“―÷Σ≈ΉΈοœΏy=ax2+bxΘ®aΓΌ0Θ©Ψ≠ΙΐAΘ®6Θ§0Θ©ΓΔBΘ®8Θ§8Θ©ΝΫΒψΘ°
Θ®1Θ©«σ≈ΉΈοœΏΒΡΫβΈω ΫΘΜ
Θ®2Θ©ΫΪ÷±œΏOBœρœ¬ΤΫ“ΤmΗωΒΞΈΜ≥ΛΕ»ΚσΘ§ΒΟΒΫΒΡ÷±œΏ”κ≈ΉΈοœΏ÷Μ”–“ΜΗωΙΪΙ≤ΒψDΘ§«σmΒΡ÷ΒΦΑΒψDΒΡΉχ±ξΘΜ
Θ®3Θ©»γΆΦ2Θ§»τΒψN‘Ύ≈ΉΈοœΏ…œΘ§«“ΓœNBO=ΓœABOΘ§‘ρ‘ΎΘ®2Θ©ΒΡΧθΦΰœ¬Θ§‘ΎΉχ±ξΤΫΟφΡΎ”–ΒψPΘ§«σ≥ωΥυ”–¬ζΉψΓςPODΓΉΓςNOBΒΡΒψPΉχ±ξΘ®ΒψPΓΔOΓΔDΖ÷±π”κΒψNΓΔOΓΔBΕ‘”ΠΘ©Θ°
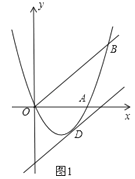
ΓΨ¥πΑΗΓΩΘ®1Θ©≈ΉΈοœΏΒΡΫβΈω Ϋ «y=![]() x2©¹3xΘΜΘ®2Θ©DΒψΒΡΉχ±ξΈΣΘ®4Θ§©¹4Θ©ΘΜΘ®3Θ©ΒψPΒΡΉχ±ξ «Θ®
x2©¹3xΘΜΘ®2Θ©DΒψΒΡΉχ±ξΈΣΘ®4Θ§©¹4Θ©ΘΜΘ®3Θ©ΒψPΒΡΉχ±ξ «Θ®![]() Θ©ΜρΘ®
Θ©ΜρΘ®![]() Θ©Θ°
Θ©Θ°
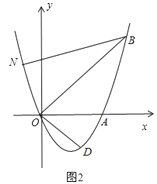
ΓΨΫβΈωΓΩ ‘ΧβΖ÷ΈωΘΚΘ®1Θ©άϊ”Ο¥ΐΕ®œΒ ΐΖ®«σΕΰ¥ΈΚ· ΐΫβΈω ΫΫχΕχΒΟ≥ω¥πΑΗΦ¥Ω…ΘΜ
Θ®2Θ© Ήœ»«σ≥ω÷±œΏOBΒΡΫβΈω ΫΈΣy=xΘ§ΫχΕχΫΪΕΰ¥ΈΚ· ΐ“‘“Μ¥ΈΚ· ΐΝΣΝΔ«σ≥ωΫΜΒψΦ¥Ω…ΘΜ
Θ®3Θ© Ήœ»«σ≥ω÷±œΏAΓδBΒΡΫβΈω ΫΘ§ΫχΕχ”…ΓςP1ODΓΉΓςNOBΘ§ΒΟ≥ωΓςP1ODΓΉΓςN1OB1Θ§ΫχΕχ«σ≥ωΒψP1ΒΡΉχ±ξΘ§‘Όάϊ”ΟΖ≠’έ±δΜΜΒΡ–‘÷ ΒΟ≥ωΝμ“ΜΒψΒΡΉχ±ξΘ°
‘ΧβΫβΈωΘΚ
Θ®1Θ©ΓΏ≈ΉΈοœΏy=ax2+bxΘ®aΓΌ0Θ©Ψ≠ΙΐAΘ®6Θ§0Θ©ΓΔBΘ®8Θ§8Θ©
ΓύΫΪA”κBΝΫΒψΉχ±ξ¥ζ»κΒΟΘΚ![]() Θ§ΫβΒΟΘΚ
Θ§ΫβΒΟΘΚ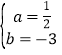 Θ§
Θ§
Γύ≈ΉΈοœΏΒΡΫβΈω Ϋ «y=![]() x2©¹3xΘ°
x2©¹3xΘ°
Θ®2Θ©…η÷±œΏOBΒΡΫβΈω ΫΈΣy=k1xΘ§”…ΒψBΘ®8Θ§8Θ©Θ§
ΒΟΘΚ8=8k1Θ§ΫβΒΟΘΚk1=1
Γύ÷±œΏOBΒΡΫβΈω ΫΈΣy=xΘ§
Γύ÷±œΏOBœρœ¬ΤΫ“ΤmΗωΒΞΈΜ≥ΛΕ»ΚσΒΡΫβΈω ΫΈΣΘΚy=x©¹mΘ§
Γύx©¹m=![]() x2©¹3xΘ§
x2©¹3xΘ§
ΓΏ≈ΉΈοœΏ”κ÷±œΏ÷Μ”–“ΜΗωΙΪΙ≤ΒψΘ§
ΓύΓς=16©¹2m=0Θ§
ΫβΒΟΘΚm=8Θ§
¥Υ ±x1=x2=4Θ§y=x2©¹3x=©¹4Θ§
ΓύDΒψΒΡΉχ±ξΈΣΘ®4Θ§©¹4Θ©
Θ®3Θ©ΓΏ÷±œΏOBΒΡΫβΈω ΫΈΣy=xΘ§«“AΘ®6Θ§0Θ©Θ§
ΓύΒψAΙΊ”Ύ÷±œΏOBΒΡΕ‘≥ΤΒψAΓδΒΡΉχ±ξ «Θ®0Θ§6Θ©Θ§
ΗυΨί÷αΕ‘≥Τ–‘÷ ΚΆ»ΐœΏΚœ“Μ–‘÷ ΒΟ≥ωΓœAΓδBO=ΓœABOΘ§
…η÷±œΏAΓδBΒΡΫβΈω ΫΈΣy=k2x+6Θ§ΙΐΒψΘ®8Θ§8Θ©Θ§
Γύ8k2+6=8Θ§ΫβΒΟΘΚk2=![]() Θ§
Θ§
Γύ÷±œΏAΓδBΒΡΫβΈω Ϋ «y=![]() Θ§
Θ§
ΓΏΓœNBO=ΓœABOΘ§ΓœAΓδBO=ΓœABOΘ§
ΓύBAΓδΚΆBN÷ΊΚœΘ§Φ¥ΒψN‘Ύ÷±œΏAΓδB…œΘ§
Γύ…ηΒψNΘ®nΘ§![]() Θ©Θ§”÷ΒψN‘Ύ≈ΉΈοœΏy=
Θ©Θ§”÷ΒψN‘Ύ≈ΉΈοœΏy=![]() x2©¹3x…œΘ§
x2©¹3x…œΘ§
Γύ![]() =
=![]() n2©¹3nΘ§ ΫβΒΟΘΚn1=©¹
n2©¹3nΘ§ ΫβΒΟΘΚn1=©¹![]() Θ§n2=8Θ®≤ΜΚœΧβ“βΘ§…α»ΞΘ©
Θ§n2=8Θ®≤ΜΚœΧβ“βΘ§…α»ΞΘ©
ΓύNΒψΒΡΉχ±ξΈΣΘ®©¹![]() Θ§
Θ§![]() Θ©Θ°
Θ©Θ°
»γΆΦ1Θ§ΫΪΓςNOB―Ίx÷αΖ≠’έΘ§ΒΟΒΫΓςN1OB1Θ§
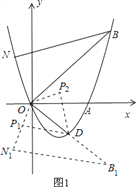
‘ρN1Θ®©¹![]() Θ§-
Θ§-![]() Θ©Θ§B1Θ®8Θ§©¹8Θ©Θ§
Θ©Θ§B1Θ®8Θ§©¹8Θ©Θ§
ΓύOΓΔDΓΔB1ΕΦ‘Ύ÷±œΏy=©¹x…œΘ°
ΓΏΓςP1ODΓΉΓςNOBΘ§ΓςNOBΓ’ΓςN1OB1Θ§
ΓύΓςP1ODΓΉΓςN1OB1Θ§
Γύ![]() Θ§
Θ§
ΓύΒψP1ΒΡΉχ±ξΈΣΘ®![]() Θ©Θ°
Θ©Θ°
ΫΪΓςOP1D―Ί÷±œΏy=©¹xΖ≠’έΘ§Ω…ΒΟΝμ“ΜΗω¬ζΉψΧθΦΰΒΡΒψP2Θ®![]() Θ©Θ§
Θ©Θ§
Ήέ…œΥυ ωΘ§ΒψPΒΡΉχ±ξ «Θ®![]() Θ©ΜρΘ®
Θ©ΜρΘ®![]() Θ©Θ°
Θ©Θ°



| ΡξΦΕ | ΗΏ÷–ΩΈ≥Χ | ΡξΦΕ | ≥θ÷–ΩΈ≥Χ |
| ΗΏ“Μ | ΗΏ“ΜΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θ“Μ | ≥θ“ΜΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
| ΗΏΕΰ | ΗΏΕΰΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θΕΰ | ≥θΕΰΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
| ΗΏ»ΐ | ΗΏ»ΐΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θ»ΐ | ≥θ»ΐΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
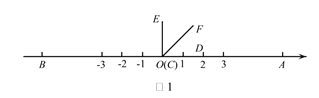
ΓΨΧβΡΩΓΩ»γΆΦ1Θ§‘Ύ ΐ÷α…œAΘ§BΝΫΒψΕ‘”ΠΒΡ ΐΖ÷±π «6Θ§-6Θ§ ![]() Θ®C”κO÷ΊΚœΘ§DΒψ‘Ύ ΐ÷αΒΡ’ΐΑκ÷α…œΘ©
Θ®C”κO÷ΊΚœΘ§DΒψ‘Ύ ΐ÷αΒΡ’ΐΑκ÷α…œΘ©
Θ®1Θ©»γΆΦ1Θ§»τCF ΤΫΖ÷![]() Θ§‘ρ
Θ§‘ρ![]() _________ΘΜ
_________ΘΜ
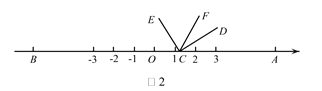
Θ®2Θ©»γΆΦ2Θ§ΫΪ![]() ―Ί ΐ÷αΒΡ’ΐΑκ÷αœρ”“ΤΫ“ΤtΘ®0ΘΦtΘΦ3Θ©ΗωΒΞΈΜΚσΘ§‘Ό»ΤΒψΕΞΒψ
―Ί ΐ÷αΒΡ’ΐΑκ÷αœρ”“ΤΫ“ΤtΘ®0ΘΦtΘΦ3Θ©ΗωΒΞΈΜΚσΘ§‘Ό»ΤΒψΕΞΒψ![]() Ρφ ±’κ–ΐΉΣ30tΕ»Θ§Ής
Ρφ ±’κ–ΐΉΣ30tΕ»Θ§Ής![]() ΤΫΖ÷
ΤΫΖ÷![]() Θ§¥Υ ±Φ«
Θ§¥Υ ±Φ«![]() .
.
ΔΌΒ±t=1 ±Θ§ ![]() _______ΘΜ
_______ΘΜ
ΔΎ≤¬œκ![]() ΚΆ
ΚΆ![]() ΒΡ ΐΝΩΙΊœΒΘ§≤Δ÷ΛΟςΘΜ
ΒΡ ΐΝΩΙΊœΒΘ§≤Δ÷ΛΟςΘΜ
Θ®3Θ©»γΆΦ3Θ§ΩΣ Φ![]() ”κ
”κ![]() ÷ΊΚœΘ§ΫΪ
÷ΊΚœΘ§ΫΪ![]() ―Ί ΐ÷αΒΡ’ΐΑκ÷αœρ”“ΤΫ“ΤtΘ®0ΘΦtΘΦ3Θ©ΗωΒΞΈΜΘ§‘Ό»ΤΒψΕΞΒψ
―Ί ΐ÷αΒΡ’ΐΑκ÷αœρ”“ΤΫ“ΤtΘ®0ΘΦtΘΦ3Θ©ΗωΒΞΈΜΘ§‘Ό»ΤΒψΕΞΒψ![]() Ρφ ±’κ–ΐΉΣ30tΕ»Θ§Ής
Ρφ ±’κ–ΐΉΣ30tΕ»Θ§Ής![]() ΤΫΖ÷
ΤΫΖ÷![]() Θ§¥Υ ±Φ«
Θ§¥Υ ±Φ«![]() Θ§”κ¥ΥΆ§ ±Θ§ΫΪ
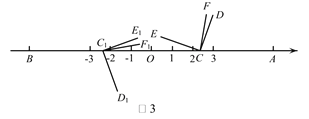
Θ§”κ¥ΥΆ§ ±Θ§ΫΪ![]() ―Ί ΐ÷αΒΡΗΚΑκ÷αœρΉσΤΫ“ΤtΘ®0ΘΦtΘΦ3Θ©ΗωΒΞΈΜΘ§‘Ό»ΤΒψΕΞΒψ
―Ί ΐ÷αΒΡΗΚΑκ÷αœρΉσΤΫ“ΤtΘ®0ΘΦtΘΦ3Θ©ΗωΒΞΈΜΘ§‘Ό»ΤΒψΕΞΒψ![]() Υ≥ ±’κ–ΐΉΣ30tΕ»Θ§Ής
Υ≥ ±’κ–ΐΉΣ30tΕ»Θ§Ής![]() ΤΫΖ÷
ΤΫΖ÷![]() Θ§Φ«
Θ§Φ«![]() Θ§»τ
Θ§»τ![]() ”κ
”κ![]() ¬ζΉψ
¬ζΉψ![]() Θ§«κ÷±Ϋ”–¥≥ωtΒΡ÷ΒΈΣ_________Θ°
Θ§«κ÷±Ϋ”–¥≥ωtΒΡ÷ΒΈΣ_________Θ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ»γΆΦΘ§‘ΎΤΫΟφ÷±Ϋ«Ήχ±ξœΒ÷–Θ§OAΓΆOBΘ§ABΓΆx÷α”ΎΒψCΘ§ΒψAΘ®![]() Θ§1Θ©‘ΎΖ¥±»άΐΚ· ΐ
Θ§1Θ©‘ΎΖ¥±»άΐΚ· ΐ![]() ΒΡΆΦœσ…œΘ°
ΒΡΆΦœσ…œΘ°

Θ®1Θ©«σΖ¥±»άΐΚ· ΐ![]() ΒΡ±μ¥ο ΫΘΜ
ΒΡ±μ¥ο ΫΘΜ
Θ®2Θ©‘Ύx÷αΒΡΗΚΑκ÷α…œ¥φ‘Ύ“ΜΒψPΘ§ ΙΒΟSΓςAOP=![]() SΓςAOBΘ§«σΒψPΒΡΉχ±ξΘΜ
SΓςAOBΘ§«σΒψPΒΡΉχ±ξΘΜ
Θ®3Θ©»τΫΪΓςBOA»ΤΒψBΑ¥Ρφ ±’κΖΫœρ–ΐΉΣ60ΓψΒΟΒΫΓςBDEΘ°÷±Ϋ”–¥≥ωΒψEΒΡΉχ±ξΘ§≤Δ≈–ΕœΒψE «Ζώ‘ΎΗΟΖ¥±»άΐΚ· ΐΒΡΆΦœσ…œΘ§ΥΒΟςάμ”…Θ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩΒγΉ”Χχ‘ι”ΈœΖ≈Χ «»γΆΦΥυ ΨΒΡΓςABCΘ§AB=AC=BC=5Θ°»γΙϊΧχ‘ιΩΣ Φ ±‘ΎBC±ΏΒΡP0¥ΠΘ§BP0=2Θ°Χχ‘ιΒΎ“Μ≤Ϋ¥”P0ΧχΒΫAC±ΏΒΡP1Θ®ΒΎ1¥Έ¬δΒψΘ©¥ΠΘ§«“CP1= CP0ΘΜΒΎΕΰ≤Ϋ¥”P1ΧχΒΫAB±ΏΒΡP2Θ®ΒΎ2¥Έ¬δΒψΘ©¥ΠΘ§«“AP2= AP1ΘΜΒΎ»ΐ≤Ϋ¥”P2ΧχΒΫBC±ΏΒΡP3Θ®ΒΎ3¥Έ¬δΒψΘ©¥ΠΘ§«“BP3= BP2ΘΜΓ≠ΘΜΧχ‘ιΑ¥’’…œ ωΙφ‘ρ“Μ÷±Χχœ¬»ΞΘ§ΒΎn¥Έ¬δΒψΈΣPnΘ®nΈΣ’ΐ’ϊ ΐΘ©Θ§‘ρΒψP2016”κΒψP2017÷°ΦδΒΡΨύάκΈΣ_________Θ°

≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ»γΆΦΥυ ΨΘ§ABΓΈDEΘ§ACΓΈDFΘ§AC=DFœ¬Ν–ΧθΦΰ÷–Θ§≤ΜΡή≈–ΕœΓςABCΓ’ΓςDEFΒΡ «Θ®ΓΓΓΓΘ©

A. AB=DE B. ΓœB=ΓœE C. EF=BC D. EFΓΈBC
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ»γΆΦΘ§‘Ύ÷±Ϋ«Ήχ±ξœΒ÷–Βψ![]() ΒΡΉχ±ξΈΣΘ®1Θ§0Θ©Θ§ΙΐΒψ
ΒΡΉχ±ξΈΣΘ®1Θ§0Θ©Θ§ΙΐΒψ![]() Ήςx÷αΒΡ¥ΙœΏΫΜ÷±œΏy=2x”Ύ
Ήςx÷αΒΡ¥ΙœΏΫΜ÷±œΏy=2x”Ύ![]() Θ§ΙΐΒψ
Θ§ΙΐΒψ![]() Ής÷±œΏy=2xΒΡ¥ΙœΏΫΜx÷α”Ύ
Ής÷±œΏy=2xΒΡ¥ΙœΏΫΜx÷α”Ύ![]() Θ§ΙΐΒψ
Θ§ΙΐΒψ![]() Ήςx÷αΒΡ¥ΙœΏΫΜ÷±œΏy=2x”Ύ
Ήςx÷αΒΡ¥ΙœΏΫΜ÷±œΏy=2x”Ύ![]() Γ≠Θ§“ά¥ΥΙφ¬…Θ§‘ρ
Γ≠Θ§“ά¥ΥΙφ¬…Θ§‘ρ![]() ΒΡΉχ±ξΈΣ___________.
ΒΡΉχ±ξΈΣ___________.

≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ»γΆΦΘ§≥ΛΖΫ–Έ÷ΫΤ§ABCD÷–Θ§ABΘΫ6 cmΘ§BCΘΫ8 cmΘ§ΒψE «BC±Ώ…œ“ΜΒψΘ§Ν§Ϋ”AEΘ§≤ΔΫΪΓςAEB―ΊAE’έΒΰΘ§ΒΟΒΫΓςAEBΓδΘ§“‘CΘ§EΘ§BΓδΈΣΕΞΒψΒΡ»ΐΫ«–Έ «÷±Ϋ«»ΐΫ«–Έ ±Θ§BEΒΡ≥ΛΈΣ____cm.

≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ»γΆΦΘ§“Μ¥ΈΚ· ΐy=-2x+2ΒΡΆΦœσ”κ![]() ÷αΓΔ
÷αΓΔ![]() ÷αΖ÷±πΫΜ”ΎΒψ
÷αΖ÷±πΫΜ”ΎΒψ![]() ΓΔ
ΓΔ![]() Θ§“‘œΏΕΈ
Θ§“‘œΏΕΈ![]() ΈΣ÷±Ϋ«±Ώ‘ΎΒΎ“ΜœσœόΡΎΉςΒ»―ϋ÷±Ϋ«»ΐΫ«–ΈABCΘ§«“
ΈΣ÷±Ϋ«±Ώ‘ΎΒΎ“ΜœσœόΡΎΉςΒ»―ϋ÷±Ϋ«»ΐΫ«–ΈABCΘ§«“![]() Θ§‘ρΒψCΉχ±ξΈΣ_____.
Θ§‘ρΒψCΉχ±ξΈΣ_____.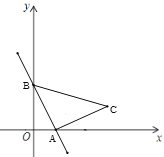
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ»γΆΦΘ§“―÷ΣΒψAΓΔBΓΔC «÷±œΏl…œΒΡ»ΐΗωΒψΘ§œΏΕΈABΘΫ8άεΟΉΘ°
Θ®1Θ©»τABΘΫ2BCΘ§«σœΏΕΈACΒΡ≥ΛΕ»ΘΜ
Θ®2Θ©»τΒψC «œΏΕΈABΒΡ÷–ΒψΘ§ΒψPΓΔQ «÷±œΏl…œΒΡΝΫΗωΕ·ΒψΘ§ΒψPΒΡΥΌΕ»ΈΣ1άεΟΉ/ΟκΘ§ΒψQΒΡΥΌΕ»ΈΣ2άεΟΉ/ΟκΘ°ΒψPΓΔQΖ÷±π¥”ΒψCΓΔBΆ§ ±≥ωΖΔ‘Ύ÷±œΏ…œ‘ΥΕ·Θ§‘ρΨ≠ΙΐΕύ…ΌΟκ ±œΏΕΈPQΒΡ≥ΛΈΣ5άεά¥ΘΩ
![]()
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΙζΦ ―ß–Θ”≈―Γ - ΝΖœΑ≤αΝ–±μ - ‘ΧβΝ–±μ
Κΰ±± ΓΜΞΝΣΆχΈΞΖ®ΚΆ≤ΜΝΦ–≈œΔΨΌ±®ΤΫΧ® | Άχ…œ”–ΚΠ–≈œΔΨΌ±®Ή®«χ | Βγ–≈’©Τ≠ΨΌ±®Ή®«χ | …φάζ Ζ–ιΈό÷ς“ε”–ΚΠ–≈œΔΨΌ±®Ή®«χ | …φΤσ«÷»®ΨΌ±®Ή®«χ
ΈΞΖ®ΚΆ≤ΜΝΦ–≈œΔΨΌ±®ΒγΜΑΘΚ027-86699610 ΨΌ±®” œδΘΚ58377363@163.com