
【题目】如图,已知点A、B、C是直线l上的三个点,线段AB=8厘米.
(1)若AB=2BC,求线段AC的长度;
(2)若点C是线段AB的中点,点P、Q是直线l上的两个动点,点P的速度为1厘米/秒,点Q的速度为2厘米/秒.点P、Q分别从点C、B同时出发在直线上运动,则经过多少秒时线段PQ的长为5厘来?
![]()
【答案】(1)12厘米;(2),经过![]() 或1或3秒或9秒时线段PQ的长为5厘米
或1或3秒或9秒时线段PQ的长为5厘米
【解析】
(1)根据线段的和差倍分即可得到结论;
(2)由于BC=4厘米,点P、Q分别从点C、点B同时出发在直线上运动,当线段PQ的长为5厘米时,可分四种情况进行讨论:点P向左、点Q向右运动;点P、Q都向右运动;点P、Q都向左运动;点P向右、点Q向左运动;都可以根据线段PQ的长为5厘米列出方程,解方程即可.
解:(1)点C在点B的左侧,如图1,

∵AB=8厘米,AB=2BC,
∴BC=4厘米,
∴AC=AB﹣BC=8﹣4=4厘米;
点C在点B的右侧,如图2,
![]()
∵AB=8厘米,AB=2BC,
∴BC=4厘米,
∴AC=AB+BC=8+4=12厘米;
(2)∵点C是线段AB的中点,
∴BC=4厘米,
设运动时间为t秒,PQ=5厘米.
①如果点P向左、点Q向右运动时,如图3,
![]()
由题意,得:t+2t=5﹣4,
解得t=![]() ;
;
②点P、Q都向右运动时,如图4,

由题意,得:2t﹣t=5﹣4,
解得t=1;
③点P向右、点Q向左运动,如图5,
![]()
由题意,得:2t﹣4+t=5,
解得t=3;
④点P、Q都向左运动,如图6

由题意,得:2t﹣t=5+4,
解得t=9.
综上所述,经过![]() 或1或3秒或9秒时线段PQ的长为5厘米.
或1或3秒或9秒时线段PQ的长为5厘米.


科目:初中数学 来源: 题型:
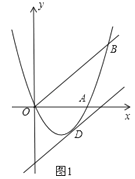
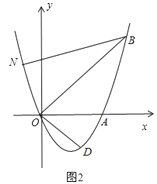
【题目】如图1,已知抛物线y=ax2+bx(a≠0)经过A(6,0)、B(8,8)两点.
(1)求抛物线的解析式;
(2)将直线OB向下平移m个单位长度后,得到的直线与抛物线只有一个公共点D,求m的值及点D的坐标;
(3)如图2,若点N在抛物线上,且∠NBO=∠ABO,则在(2)的条件下,在坐标平面内有点P,求出所有满足△POD∽△NOB的点P坐标(点P、O、D分别与点N、O、B对应).
查看答案和解析>>
科目:初中数学 来源: 题型:
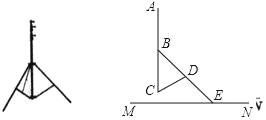
【题目】某数码产品专卖店的一块摄像机支架如图所示,将该支架打开立于地面MN上,主杆AC与地面垂直,调节支架使得脚架BE与主杆AC的夹角∠CBE=45°,这时支架CD与主杆AC的夹角∠BCD恰好等于60°,若主杆最高点A到调节旋钮B的距离为40cm.支架CD的长度为30cm,旋转钮D是脚架BE的中点,求脚架BE的长度和支架最高点A到地面的距离.(结果保留根号)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某体育用品商场采购员要到厂家批发购买篮球和排球共![]() 个,篮球个数不少于排球个数,付款总额不得超过
个,篮球个数不少于排球个数,付款总额不得超过![]() 元,已知两种球厂的批发价和商场的零售价如下表. 设该商场采购
元,已知两种球厂的批发价和商场的零售价如下表. 设该商场采购![]() 个篮球.
个篮球.
品名 | 厂家批发价/元/个 | 商场零售价/元/个 |
篮球 |
|
|
排球 |
|
|
(1)求该商场采购费用![]() (单位:元)与
(单位:元)与![]() (单位:个)的函数关系式,并写出自变最
(单位:个)的函数关系式,并写出自变最![]() 的取值范围:
的取值范围:
(2)该商场把这![]() 个球全都以零售价售出,求商场能获得的最大利润;
个球全都以零售价售出,求商场能获得的最大利润;
(3)受原材料和工艺调整等因素影响,采购员实际采购时,低球的批发价上调了![]() 元/个,同时排球批发价下调了
元/个,同时排球批发价下调了![]() 元/个.该体有用品商场决定不调整商场零售价,发现将
元/个.该体有用品商场决定不调整商场零售价,发现将![]() 个球全部卖出获得的最低利润是
个球全部卖出获得的最低利润是![]() 元,求
元,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
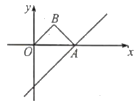
【题目】如图,直线y=x﹣4与x轴交于点A,以OA为斜边在x轴上方作等腰Rt△OAB,并将Rt△AOB沿x轴向右平移,当点B落在直线y=x﹣4上时,Rt△OAB扫过的面积是__.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】用同样大小的黑色棋子按如图所示的规律摆放:

(1)分别写出第6、7两个图形各有多少颗黑色棋子?
(2)写出第n个图形黑色棋子的颗数?
(3)是否存在某个图形有1020颗黑色棋子?若存在,求出是第几个图形;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图在平面直角坐标系中,若干个半径为2个单位长度,圆心角为60°的扇形组成一条连续的曲线,点P从原点O出发,沿这条曲线向右上下起伏运动,点在直线上的速度为每秒2个单位长度,点在弧线上的速度为每秒![]() 个单位长度,则2018秒时,点P的坐标是( )
个单位长度,则2018秒时,点P的坐标是( )
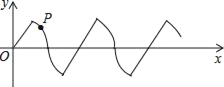
A. (2017,0) B. (2017, ![]() ) C. (2018,0) D. (2019,﹣
) C. (2018,0) D. (2019,﹣![]() )
)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com