
【题目】如图,函数![]() 的图象经过
的图象经过![]() ,
,![]() ,其中
,其中![]() ,过点A作x轴的垂线,垂足为C,过点B作y轴的垂线,垂足为D,连结AD,DC,CB,AC与BD相交于点E.
,过点A作x轴的垂线,垂足为C,过点B作y轴的垂线,垂足为D,连结AD,DC,CB,AC与BD相交于点E.

(1)若![]() 的面积为4,求点B的坐标;
的面积为4,求点B的坐标;
(2)四边形ABCD能否成为平行四边形,若能,求点B的坐标,若不能说明理由;
(3)当![]() 时,求证:四边形ABCD是等腰梯形.
时,求证:四边形ABCD是等腰梯形.
【答案】(1)![]() ;(2)能,
;(2)能, ![]() ;(3)详见解析.
;(3)详见解析.
【解析】
(1)将A的坐标代入反比例解析式中求出k的值,确定出反比例解析式,将B的坐标代入反比例解析式中,求出mn的值,三角形ABD的面积由BD为底边,AE为高,利用三角形面积公式来求,由B的坐标得到BD=m,由AC-EC表示出AE,由已知的面积,利用面积公式列出关系式,将mn的值代入,求出m的值,进而确定出n的值,即可得到B的坐标;
(2)假设四边形ABCD为平行四边形,利用平行四边形的性质得到BD与AC互相平分,得到E为AC的中点,E为BD的中点,由A的坐标求出E的坐标,进而确定出B的坐标,将B坐标代入反比例解析式检验,B在反比例图象上,故假设正确,四边形ABCD能为平行四边形;
(3)由由AC=BD,得到A的纵坐标与B的横坐标相等,确定出B的横坐标,将B横坐标代入反比例解析式中求出B的纵坐标,得到B的坐标,进而确定出E的坐标,得到DE=CE=1,由AC=BD,利用等式的性质得到AE=BE,进而得到两对对应边成比例,且由对顶角相等得到夹角相等,利用两边对应成比例且夹角相等的两三角形相似,得到三角形DEC与三角形AEB相似,由相似三角形的对应角相等得到一对内错角相等,利用内错角相等两直线平行得到CD与AB平行,而在直角三角形ADE与直角三角形BEC中,DE=EC,AE=BE,利用勾股定理得到AD=BC,且AD与BC不平行,可得出四边形ABCD为等腰梯形.
解:(1)![]() ;
;
(2)若ABCD是平行四边形,则AC,BD互相平分,
∵![]() ,∴
,∴![]() ,
,![]()
将![]() 代入反比例中,
代入反比例中,![]() ;
;
∴B在![]() 上,则四边形ABCD能成为平行四边形;
上,则四边形ABCD能成为平行四边形;
(3)∵![]() ,
,![]() ,
,![]() ;
;
∴![]()
∵![]() 轴,
轴,![]() 轴,
轴,
∴![]()
∴![]()
∵![]()
∴![]()
∴![]()
∴![]()
∴![]()
∴![]()
根据勾股定理,![]() .
.
∵AD与BC不平行
∴则四边形ABCD是等腰梯形.


 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案科目:初中数学 来源: 题型:
【题目】为节约用水,某市规定三口之家每月标准用水量为![]() 立方米,超过部分加价收费,假设不超过部分水费为
立方米,超过部分加价收费,假设不超过部分水费为![]() 元/立方米,超过部分水费为
元/立方米,超过部分水费为![]() 元/立方米.
元/立方米.
![]() 请用代数式分别表示这家按标准用水和超出标准用水各应缴纳的水费;
请用代数式分别表示这家按标准用水和超出标准用水各应缴纳的水费;
![]() 如果这家某月用水
如果这家某月用水![]() 立方米,那么该月应交多少水费?
立方米,那么该月应交多少水费?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示是一个正方体的表面展开图,请回答下列问题:

(1)与面B、面C相对的面分别是 和 ;
(2)若A=a3+![]() a2b+3,B=﹣
a2b+3,B=﹣![]() a2b+a3,C=a3﹣1,D=﹣
a2b+a3,C=a3﹣1,D=﹣![]() (a2b+15),且相对两个面所表示的代数式的和都相等,求E、F代表的代数式.
(a2b+15),且相对两个面所表示的代数式的和都相等,求E、F代表的代数式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,观察由棱长为 ![]() 的小立方体摆成的图形,寻找规律:如图 ① 中,共有
的小立方体摆成的图形,寻找规律:如图 ① 中,共有 ![]() 个小立方体,其中
个小立方体,其中 ![]() 个看得见,
个看得见, ![]() 个看不见;如图 ② 中,共有
个看不见;如图 ② 中,共有 ![]() 个小立方体,其中
个小立方体,其中 ![]() 个看得见,
个看得见, ![]() 个看不见;如图 ③ 中,共有
个看不见;如图 ③ 中,共有 ![]() 个小立方体,其中
个小立方体,其中 ![]() 个看得见,
个看得见, ![]() 个看不见;
个看不见; ![]() ,则第 ⑥个图中,看得见的小立方体有________________个.
,则第 ⑥个图中,看得见的小立方体有________________个.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知![]() ∥
∥![]() ,点
,点![]() 、
、![]() 分别是
分别是![]() 、
、![]() 上的两点,点
上的两点,点![]() 在
在![]() 、
、![]() 之间,连接
之间,连接![]() 、
、![]() .
.
(1)如图①,若![]() ,求
,求![]() 的度数;
的度数;
(2)如图②,若点![]() 是
是![]() 下方一点,
下方一点,![]() 平分
平分![]() ,
,![]() 平分
平分![]() ,已知
,已知![]() ,求
,求![]() 的度数;
的度数;
(3)如图③,若点![]() 是
是![]() 上方一点,连接
上方一点,连接![]() 、
、![]() ,且
,且![]() 的延长线
的延长线![]() 平分
平分![]() ,
,![]() 平分
平分![]() ,
,![]() ,求
,求![]() 的度数.
的度数.



查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】数学课上, 老师要求同学们利用三角板画两条平行线.老师说苗苗和小华两位同学画法都是正确的,两位同学的画法如下:
苗苗的画法:

①将含30°角的三角尺的最长边与直线a重合,另一块三角尺最长边与含30°角的三角尺的最短边紧贴;
②将含30°角的三角尺沿贴合边平移一段距离,画出最长边所在直线b,则b//a.
小华的画法:
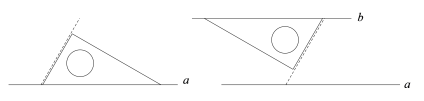
①将含30°角三角尺的最长边与直线a重合,用虚线做出一条最短边所在直线;
②再次将含30°角三角尺的最短边与虚线重合,画出最长边所在直线b,则b//a.
请在苗苗和小华两位同学画平行线的方法中选出你喜欢的一种,并写出这种画图的依据.
答:我喜欢__________同学的画法,画图的依据是__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们知道,正整数的和1+3+5+…+(2n﹣1)=n2,若把所有正偶数从小到大排列,并按如下规律分组:(2),(4,6,8),(10,12,14,16,18),(20,22,24,26,28,30,32),…,现有等式Am=(i,j)表示正偶数m是第i组第j个数(从左到右数),如A8=(2,3),则A2018=_____
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com