
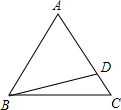
 如图所示,在△ABC中,AB=AC,点D在AC上(不与A,C重合),BD=AB,求∠A的取值范围.
如图所示,在△ABC中,AB=AC,点D在AC上(不与A,C重合),BD=AB,求∠A的取值范围. 分析 根据等腰三角形两底角相等用∠A表示出∠ABC、∠ABD,然后列不等式求解,再根据三角形的内角和定理判断出∠A为锐角,然后写出即可.
解答 解:∵AB=AC,
∴∠ABC=$\frac{1}{2}$(180°-∠A),
∵BD=AB,
∴∠ABD=180°-2∠A,
由图可知,∠ABC>∠ABD,
∴$\frac{1}{2}$(180°-∠A)>180°-2∠A,
∴∠A>60°,
在△ABD中,由三角形的内角和定理,∠A<90°,
∴∠A的取值范围是60°<∠A<90°.
点评 本题考查了等腰三角形的性质,主要利用了等腰三角形两底角相等的性质,易错点是利用三角形的内角和定理判断出∠A是锐角.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
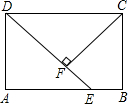 如图,四边形ABCD是矩形,E是AB上一点,且DE=AB,过点C作CF⊥DE,垂足为E.
如图,四边形ABCD是矩形,E是AB上一点,且DE=AB,过点C作CF⊥DE,垂足为E.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| a | 0.000 001 | 0.001 | 1 | 1000 | 1000 000 |
| $\root{3}{a}$ | 0.01 | 0.1 | 1 | 10 | 100 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com