
| A地 | B地 | C地 | 合计 | |
| 产品件数/件 | x | 200-3x | 2x | 200 |
| 运费/元 | 25x | 1600-24x | 50x | 56x+1600 |
分析 (1)①根据n=200求出运往B第的件数,再分别乘以单价即可求出运往B地、C地的运费;
②根据运往B地的件数不多于运往C地的件数,总运费不超过4000元列出不等式组,然后求解得到x的取值范围,再根据x是正整数确定出运输方案;
(2)根据总运费列出算式并用x表示出n,再根据n不小于运往A、C两地的件数求出x的取值范围,然后根据一次函数的增减性求出n的最小值即可.
解答 解:(1)①根据信息填表: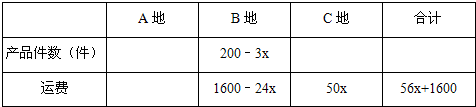 ;
;
②由题意,得$\left\{\begin{array}{l}{200-3x≤2x①}\\{30x+1600-24x+50x≤4000②}\end{array}\right.$,
解不等式①得,x≥40,
解不等式②得,x≤42$\frac{6}{7}$,
所以,40≤x≤42$\frac{6}{7}$,
∵x为整数,
∴x=40或41或42,
∴有三种方案,分别是:方案一:A地40件,B地80件,C地80件;
方案二:A地41件,B地77件,C地82件;
方案三:A地42件,B地74件,C地84件;
(2)由题意,得30x+8(n-3x)+50x=5800,
整理,得n=725-7x,
∵n-3x≥0,
∴725-7x-3x≥0,
解得x≤72.5,
又∵x≥0,
∴0≤x≤72.5且x为整数,
∵n随x的增大而减少,
∴当x=72时,n有最小值为725-7×72=221.
点评 本题考查的是用一次函数解决实际问题,此类题是近年中考中的热点问题.注意利用一次函数求最值时,关键是应用一次函数的性质;即由函数y随x的变化,结合自变量的取值范围确定最值.


科目:初中数学 来源:2016-2017学年度海南省九年级第二次月考数学试卷(解析版) 题型:单选题
如图,修建抽水站时,沿着坡度为i=1:6的斜坡铺设管道. 下列等式成立的是( )
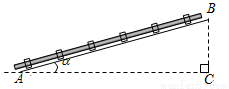
A. sinα =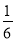 B. cosα=
B. cosα=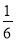 C. tanα=
C. tanα=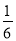 D. tanα=2
D. tanα=2
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 抛掷一枚硬币,硬币落地时正面朝上是随机事件 | |
| B. | 把4个球放入三个抽屉中,其中一个抽屉中至少有2个球是必然事件 | |
| C. | 任意打开七年级下册数学教科书,正好是97页是随机事件 | |
| D. | 某种彩票的中奖率为0.001,则买100张彩票一定有1张中奖 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
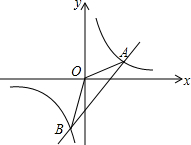 如图,已知一次函数y=kx-3的图象与反比例函数y=$\frac{m}{x}$(m为常数,且m≠0)的图象交于A、B两点,点A的坐标为(4,1);
如图,已知一次函数y=kx-3的图象与反比例函数y=$\frac{m}{x}$(m为常数,且m≠0)的图象交于A、B两点,点A的坐标为(4,1);查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. |  | B. |  | C. |  | D. |  |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
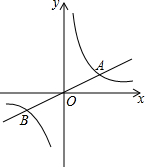 如图,已知直线y1=$\frac{1}{2}$x与双曲线y2=$\frac{k}{x}$(k>0)交于A、B两点,且点A的横坐标为4.
如图,已知直线y1=$\frac{1}{2}$x与双曲线y2=$\frac{k}{x}$(k>0)交于A、B两点,且点A的横坐标为4.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com