
分析 先根据反比例函数与一次函数的交点坐标满足两函数的解析式得到$\frac{1}{x}$=x+2,去分母化为一元二次方程得到x2+2x-1=0,根据根与系数的关系得到a+b=-2,ab=-1,然后变形$\frac{1}{a}$+$\frac{1}{b}$得$\frac{a+b}{ab}$,再利用整体思想计算即可.
解答 解:根据题意得$\frac{1}{x}$=x+2,化为整式方程,整理得x2+2x-1=0,
∵函数y=$\frac{1}{x}$与y=x+2图象交点横坐标分别为a与b,
∴a、b为方程x2+2x-1=0的两根,
∴a+b=-2,ab=-1,
∴$\frac{1}{a}$+$\frac{1}{b}$=$\frac{a+b}{ab}$=$\frac{-2}{-1}$=2.
故答案为:2.
点评 本题考查了反比例函数与一次函数的交点问题:反比例函数与一次函数的交点坐标满足两函数的解析式.也考查了一元二次方程根与系数的关系.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:选择题
| A. | $\frac{180}{x}$-$\frac{180}{x+2}$=3 | B. | $\frac{180}{x+2}$-3180x=3 | C. | $\frac{180}{x}$-$\frac{180}{x-2}$=3 | D. | $\frac{180}{x-2}$-$\frac{180}{x}$=3 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
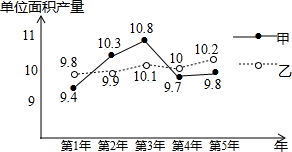 甲、乙两种水稻品种经过连续5年试验种植,每年的单位面积产量的折线图如图所示,经过计算,甲的单位面积平均产量$\overline{x}$甲=10,乙的单位面积平均产量$\overline{x}$乙=10,则根据图表估计,两种水稻品种产量比较稳定的是乙.
甲、乙两种水稻品种经过连续5年试验种植,每年的单位面积产量的折线图如图所示,经过计算,甲的单位面积平均产量$\overline{x}$甲=10,乙的单位面积平均产量$\overline{x}$乙=10,则根据图表估计,两种水稻品种产量比较稳定的是乙.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 若AB∥CD,AB=CD,则四边形ABCD是平行四边形 | |
| B. | 若AC⊥BD,AC=BD,则四边形ABCD是矩形 | |
| C. | 若AC⊥BD,AB=AD,CB=CD则四边形ABCD是菱形 | |
| D. | 若AB=BC=CD=AD,则四边形ABCD是正方形 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 绵阳市理想房价调查(元/平方米) | 百分比 |
| 3000~4000 | m |
| 4000~5000 | 30% |
| 5000~6000 | 18% |
| 6000~7000 | 7% |
| 7000~8000 | 3% |
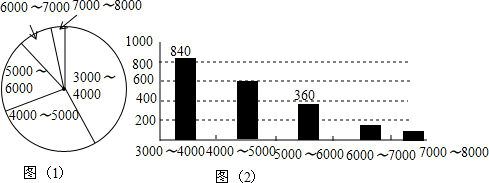
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| A地 | B地 | C地 | 合计 | |
| 产品件数/件 | x | 200-3x | 2x | 200 |
| 运费/元 | 25x | 1600-24x | 50x | 56x+1600 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
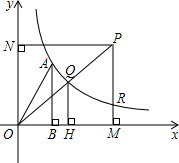 如图,曲线y=$\frac{k}{x}$(x>0)经过点A(1,2),过点A作AB⊥x轴于点B,连接OA.点P为第一象限内曲线上方一动点,过点P分别作PM⊥x轴于点M,PN⊥y轴于点N,PM交曲线于点R.连接PO交曲线于点Q,过点Q作QH⊥x轴于点H.
如图,曲线y=$\frac{k}{x}$(x>0)经过点A(1,2),过点A作AB⊥x轴于点B,连接OA.点P为第一象限内曲线上方一动点,过点P分别作PM⊥x轴于点M,PN⊥y轴于点N,PM交曲线于点R.连接PO交曲线于点Q,过点Q作QH⊥x轴于点H.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com