
【题目】如图,在菱形ABCD中,对角线AC,BD交于点O,AE⊥BC交CB延长线于E,CF∥AE交AD延长线于点F.

(1)求证:四边形AECF为矩形;
(2)连接OE,若AE=4,AD=5,求tan∠OEC的值.
 寒假乐园北京教育出版社系列答案
寒假乐园北京教育出版社系列答案科目:初中数学 来源: 题型:
【题目】小李在景区销售一种旅游纪念品,已知每件进价为6元,当销售单价定为8元时,每天可以销售200件.市场调查反映:销售单价每提高1元,日销量将会减少10件,物价部门规定:销售单价不能超过12元,设该纪念品的销售单价为x(元),日销量为y(件),日销售利润为w(元).
(1)求y与x的函数关系式.
(2)要使日销售利润为720元,销售单价应定为多少元?
(3)求日销售利润w(元)与销售单价x(元)的函数关系式,当x为何值时,日销售利润最大,并求出最大利润.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,BD是△ABC的角平分线,过点D作DE∥BC交AB于点E,DF∥AB交BC于点F.
(1)求证:四边形BEDF为菱形;
(2)如果∠A=90°,∠C=30°,BD=12,求菱形BEDF的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列命题是假命题的是( )
A.三角形的外心到三角形的三个顶点的距离相等
B.如果等腰三角形的两边长分别是5和6,那么这个等腰三角形的周长为16
C.将一次函数y=3x-1的图象向上平移3个单位,所得直线不经过第四象限
D.若关于x的一元一次不等式组![]() 无解,则m的取值范围是
无解,则m的取值范围是![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知B港口位于A观测点北偏东45°方向,且其到A观测点正北风向的距离BM的长为10![]() km,一艘货轮从B港口沿如图所示的BC方向航行4
km,一艘货轮从B港口沿如图所示的BC方向航行4![]() km到达C处,测得C处位于A观测点北偏东75°方向,则此时货轮与A观测点之间的距离AC的长为( )km.
km到达C处,测得C处位于A观测点北偏东75°方向,则此时货轮与A观测点之间的距离AC的长为( )km.

A.8![]() B.9
B.9![]() C.6
C.6![]() D.7
D.7![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
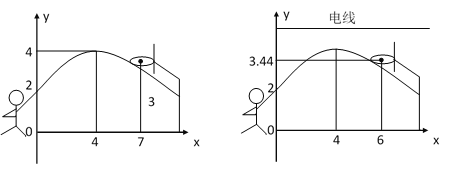
【题目】在小明的一次投篮中,球出手时离地面高2米,与篮圈中心的水平距离为7米,当球出手后水平距离为4米时到达最大高度4米.篮球运行的轨迹为抛物线,篮球中心距离地面3米,通过计算说明此球能否投中.
探究一:若出手的角度、力度和高度都不变的情况下,求小明朝着篮球架再向前平移多少米后跳起投篮也能将篮球投入篮筐中?
探究二:若出手的角度、力度和高度都发生改变的情况下,但是抛物线的顶点等其他条件不变,求小明出手的高度需要增加多少米才能将篮球投入篮筐中?
探究三:若出手的角度、力度都改变,出手高度不变,篮筐的坐标为(6,3.44),球场上方有一组高6米的电线,要想在篮球不触碰电线的情况下,将篮球投入篮筐中,直接写出二次函数解析式中a的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
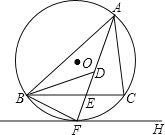
【题目】如图,![]() 是锐角
是锐角![]() 的外接圆,
的外接圆,![]() 是
是![]() 的切线,切点为
的切线,切点为![]() ,
,![]() ,连结
,连结![]() 交
交![]() 于
于![]() ,
,![]() 的平分线
的平分线![]() 交
交![]() 于
于![]() ,连结
,连结![]() .下列结论:①
.下列结论:①![]() 平分
平分![]() ;②连接
;②连接![]() ,点
,点![]() 为
为![]() 的外心;③
的外心;③![]() ;④若点
;④若点![]() ,
,![]() 分别是
分别是![]() 和
和![]() 上的动点,则
上的动点,则![]() 的最小值是
的最小值是![]() .其中一定正确的是__________(把你认为正确结论的序号都填上).
.其中一定正确的是__________(把你认为正确结论的序号都填上).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,反比例函数的图象经过点A、P,点A(6,![]() ),点P的横坐标是2.抛物线y=ax2+bx+c(a≠0)经过坐标原点,且与x轴交于点B,顶点为P.
),点P的横坐标是2.抛物线y=ax2+bx+c(a≠0)经过坐标原点,且与x轴交于点B,顶点为P.
求:(1)反比例函数的解析式;
(2)抛物线的表达式及B点坐标.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com