
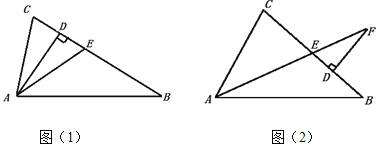
【题目】(1)如图(1),在△ABC中,AD、AE分别是△ABC的高和角平分线,已知:∠B=30°,∠C=50°.求∠DAE的度数;
(2)如图(2),∠BAC的角平分线AF交BC于点E,过点F作FD⊥BC于点D,若∠B = x°,∠C =(x+30)° .
①∠CAE = (含x的代数式表示)②求∠F的度数.
【答案】(1)∠DAE = 10° ;(2) ①∠CAE = (75-x) °,② ∠F =15°
【解析】试题分析:(1)先根据三角形内角和得到∠CAB=180°-∠B-∠C=100°,再根据角平分线与高线的定义得到∠CAE=![]() ∠CAB=50°,∠ADC=90°,则∠CAD=90°-∠C=40°,然后利用∠DAE=∠CAE-∠CAD计算即可;
∠CAB=50°,∠ADC=90°,则∠CAD=90°-∠C=40°,然后利用∠DAE=∠CAE-∠CAD计算即可;
(2)根据题意可知∠B=x°,∠C=(x+30)°,根据三角形的内角和定理可知∠ADC+∠DAC+∠C=180°,∠ADC=∠B+∠BAF,根据角平分线的性质,可知∠EAC=∠BAF,可得出∠ADC的度数,再根据FD⊥BC,可得出∠F的度数.
试题解析:(1)∵∠B=30°,∠C=50°,
∴∠CAB=180°-∠B-∠C=100°,
∵AD是△ABC角平分线,
∴∠CAE=![]() ∠CAB=50°,
∠CAB=50°,
∵AE是△ABC的高,
∴∠ADC=90°,
∴∠CAD=90°-∠C=40°,
∴∠DAE=∠CAE-∠CAD=50°-40°=10°;
(2)①∵∠B=x°,∠C=(x+30)°,AF平分∠BAC,
∴∠EAC=∠BAF,
∴∠CAE=![]() ×[180°-x°-(x+30)°]=75°-x°,
×[180°-x°-(x+30)°]=75°-x°,
②∠AEC=∠BAE+∠B=75°,
∵FD⊥BC,
∴∠F=15°.


科目:初中数学 来源: 题型:
【题目】在四边形ABCD中,已知AB∥DC,AB=DC,在不添加任何辅助线的前提下,要想该四边形为矩形,只需加上的一个条件是___(填上你认为正确的一个答案即可).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某儿童服装店欲购进A、B两种型号的儿童服装.经调查:B型号童装的进货单价是A型号童装的进货单价的两倍,购进A型号童装60件和B型号童装40件共用去2100元.
(1)、求A、B两种型号童装的进货单价各是多少元?
(2)、若该店每销售1件A型号童装可获利4元,每销售1件B型号童装可获利9元,该店准备用不超过6300元购进A、B两种型号童装共300件,且这两种型号童装全部售出后总获利不低于1795元.问该店应该怎样安排进货,才能使总获利最大?最大总获利为多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
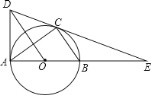
【题目】如图,⊙O是△ABC的外接圆,AB是直径,作OD∥BC与过点A的切线交于点D,连接DC并延长交AB的延长线于点E.(1)、求证:DE是⊙O的切线;(2)、若AE=6,CE=![]() ,求线段CE、BE与劣弧BC所围成的图形面积.(结果保留根号和π)
,求线段CE、BE与劣弧BC所围成的图形面积.(结果保留根号和π)
查看答案和解析>>
科目:初中数学 来源: 题型:
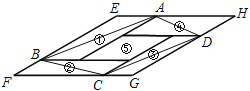
【题目】如图,①②③④⑤五个平行四边形拼成一个含30°内角的菱形EFGH(不重叠无缝隙).若①②③④四个平行四边形面积的和为14cm2,四边形ABCD面积是11cm2,则①②③④四个平行四边形周长的总和为( )
A.48cm B.36cm C.24cm D.18cm
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com