
 如图,在平面直角坐标系中,点A在函数y=-$\frac{2}{x}$(x<0)的图象上,点B在函数y=$\frac{4}{x}$(x>0)的图象上,点C在x轴上.若四边形OABC为平行四边形,则△OBC的面积为3.
如图,在平面直角坐标系中,点A在函数y=-$\frac{2}{x}$(x<0)的图象上,点B在函数y=$\frac{4}{x}$(x>0)的图象上,点C在x轴上.若四边形OABC为平行四边形,则△OBC的面积为3. 分析 首先设A(a,b),B(x,b),根据反比例函数关系式求出a与x的关系,从而得到AB=CO的长,再利用平行四边形面积公式算出面积即可.
解答 解:过A作AE⊥x轴于点E,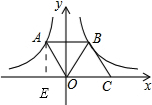
设A(a,b),B(x,b),
∵点A在反比例函数y=-$\frac{2}{x}$上,点B在反比例函数y=$\frac{4}{x}$上,
∴ab=-2,xb=4,
∴x=-2a,
∴AB=|-2a-a|=3a,
∵四边形OABC是平行四边形,
∴CO=AB=3a,
∴四边形OABC的面积是:CO•BE=6ab=6,
△OBC的面积为=3,
故答案为:3.
点评 此题主要考查了反比例函数,关键是利用反比例函数关系式表示出A、B两点的坐标,求出CO的长.


科目:初中数学 来源: 题型:填空题
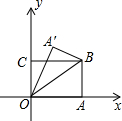 如图,四边形0ABC为矩形,A在x轴上,C在y轴上,B点坐标为(4,3),将△OAB沿OB翻折,A的对应点为A′,0A′交BC于D,则D点的坐标为($\frac{7}{8}$,3).
如图,四边形0ABC为矩形,A在x轴上,C在y轴上,B点坐标为(4,3),将△OAB沿OB翻折,A的对应点为A′,0A′交BC于D,则D点的坐标为($\frac{7}{8}$,3).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
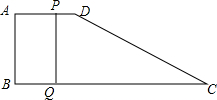 如图,在四边形ABCD中,AD∥BC,且AD<BC,AD=10cm,AB=12cm,BC=18cm,CD=15cm,动点P,Q分别从点A、C同时出发,点P以2cm/s的速度由点A向点B运动,点Q以3cm/s的速度由点C向点B运动.
如图,在四边形ABCD中,AD∥BC,且AD<BC,AD=10cm,AB=12cm,BC=18cm,CD=15cm,动点P,Q分别从点A、C同时出发,点P以2cm/s的速度由点A向点B运动,点Q以3cm/s的速度由点C向点B运动.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
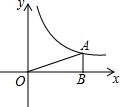 如图,反比例函数y=$\frac{k}{x}$的图象经过点A(4,b).过点A作AB⊥x轴于点B,△AOB的面积为2.求:
如图,反比例函数y=$\frac{k}{x}$的图象经过点A(4,b).过点A作AB⊥x轴于点B,△AOB的面积为2.求:查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
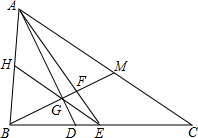 如图,在△ABC中,AC>AB,AD是角平分线,AE是中线,BF⊥AD于点G,交AE于点F,交AC于点M,EG的延长线交AB于点H.
如图,在△ABC中,AC>AB,AD是角平分线,AE是中线,BF⊥AD于点G,交AE于点F,交AC于点M,EG的延长线交AB于点H.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
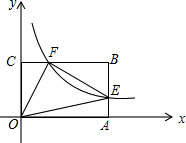 如图,在直角坐标系中,双曲线y=$\frac{2}{x}$(x>0)与矩形OABC的边AB、BC分别交于E、F,AB=nAE(n≥2),m=$\frac{{S}_{△BEF}}{{S}_{△OEF}}$.
如图,在直角坐标系中,双曲线y=$\frac{2}{x}$(x>0)与矩形OABC的边AB、BC分别交于E、F,AB=nAE(n≥2),m=$\frac{{S}_{△BEF}}{{S}_{△OEF}}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com