
【题目】如图,CD是⊙O的弦,AB是直径,且CD∥AB,连接AC、AD、OD,其中AC=CD,过点B的切线交CD的延长线于E.
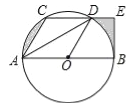
(1)求证:DA平分∠CDO;
(2)若AB=12,求图中阴影部分的周长之和(参考数据:π=3.1,![]() =1.4,
=1.4,![]() =1.7).
=1.7).
【答案】(1)详见解析;(2)26.5.
【解析】
试题分析:(1)根据平行线的性质和等腰三角形的性质可得∠CDA=∠DAO,∠DAO=∠ADO,即可证得结论.(2)易证∠CDA=∠BAD=∠CAD,可得![]() =
=![]() =
=![]() ,再证明∠DOB=60°,即可得△BOD是等边三角形,由此即可解决问题.
,再证明∠DOB=60°,即可得△BOD是等边三角形,由此即可解决问题.
试题解析:证明:(1)∵CD∥AB,
∴∠CDA=∠BAD,
又∵OA=OD,
∴∠ADO=∠BAD,
∴∠ADO=∠CDA,
∴DA平分∠CDO.
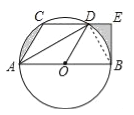
(2)如图,连接BD,
∵AB是直径,
∴∠ADB=90°,
∵AC=CD,
∴∠CAD=∠CDA,
又∵CD∥AB,
∴∠CDA=∠BAD,
∴∠CDA=∠BAD=∠CAD,
∴![]() =
=![]() =
=![]() ,
,
又∵∠AOB=180°,
∴∠DOB=60°,
∵OD=OB,
∴△DOB是等边三角形,
∴BD=OB=![]() AB=6,
AB=6,
∵![]() =
=![]() ,
,
∴AC=BD=6,
∵BE切⊙O于B,
∴BE⊥AB,
∴∠DBE=∠ABE﹣∠ABD=30°,
∵CD∥AB,
∴BE⊥CE,
∴DE=![]() BD=3,BE=BD×cos∠DBE=6×
BD=3,BE=BD×cos∠DBE=6×![]() =3
=3![]() ,
,
∴![]() 的长=
的长=![]() =2π,
=2π,
∴图中阴影部分周长之和为2π+6+2π+3+3![]() =4π+9+3
=4π+9+3![]() =4×3.1+9+3×1.7=26.5.
=4×3.1+9+3×1.7=26.5.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】如图,已知抛物线经过原点O,顶点为A(1,1),且与直线y=x﹣2交于B,C两点.
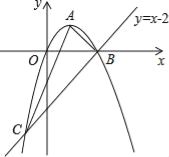
(1)求抛物线的解析式及点C的坐标;
(2)求证:△ABC是直角三角形;
(3)若点N为x轴上的一个动点,过点N作MN⊥x轴与抛物线交于点M,则是否存在以O,M,N为顶点的三角形与△ABC相似?若存在,请求出点N的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】要了解全校学生的课外作业负担情况,你认为以下抽样方法中比较合理的是( )
A. 调查全体女生 B. 调查全体男生
C. 调查九年级全体学生 D. 调查七,八,九年级各100名学生
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线y=x2+(2m+1)x+m(m﹣3)(m为常数,﹣1≤m≤4).A(﹣m﹣1,y1),B(![]() ,y2),C(﹣m,y3)是该抛物线上不同的三点,现将抛物线的对称轴绕坐标原点O逆时针旋转90°得到直线a,过抛物线顶点P作PH⊥a于H.
,y2),C(﹣m,y3)是该抛物线上不同的三点,现将抛物线的对称轴绕坐标原点O逆时针旋转90°得到直线a,过抛物线顶点P作PH⊥a于H.
(1)用含m的代数式表示抛物线的顶点坐标;
(2)若无论m取何值,抛物线与直线y=x﹣km(k为常数)有且仅有一个公共点,求k的值;
(3)当1<PH≤6时,试比较y1,y2,y3之间的大小.
查看答案和解析>>
科目:初中数学 来源: 题型:
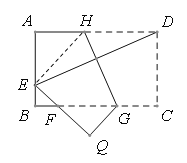
【题目】如图,将矩形ABCD沿GH对折,点C落在Q处,点D落在AB边上E处,EQ与BC相交于F,若AD=8 cm,AB=6 cm,AE=4cm,则△EBF的周长是______________ cm.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com