
����Ŀ����֪������y=x2+��2m+1��x+m��m��3����mΪ��������1��m��4����A����m��1��y1����B��![]() ��y2����C����m��y3���Ǹ��������ϲ�ͬ�����㣬�ֽ������ߵĶԳ���������ԭ��O��ʱ����ת90��õ�ֱ��a���������߶���P��PH��a��H��
��y2����C����m��y3���Ǹ��������ϲ�ͬ�����㣬�ֽ������ߵĶԳ���������ԭ��O��ʱ����ת90��õ�ֱ��a���������߶���P��PH��a��H��
��1���ú�m�Ĵ���ʽ��ʾ�����ߵĶ������ꣻ
��2��������mȡ��ֵ����������ֱ��y=x��km��kΪ���������ҽ���һ�������㣬��k��ֵ��
��3����1��PH��6ʱ���ԱȽ�y1��y2��y3֮��Ĵ�С��
���𰸡���1���������꣨��![]() ����
����![]() ������2��k=3����3����1��m����
������2��k=3����3����1��m����![]() ��
��![]() ��m��
��m��![]() ʱ����y2��y1=y3����
ʱ����y2��y1=y3����![]() ��m����
��m����![]() ʱ����y2��y1=y3��
ʱ����y2��y1=y3��
��������
�����������1�����ݶ������깫ʽ��ʾ���������꼴�ɣ���2������������ʽ�������һ��һԪ���η��̣�������=0������kֵ����3������֤��y1=y3���ٸ��ݵ�B��λ�ã��������ۣ�����![]() ����m��1�����m�ķ�Χ�����жϣ�����
����m��1�����m�ķ�Χ�����жϣ�����![]() =��m��1����A��B�غϣ������β������⣬����������
=��m��1����A��B�غϣ������β������⣬����������![]() ����m��1�����m�ķ�Χ�����жϣ�������
����m��1�����m�ķ�Χ�����жϣ�������![]() ��
��![]() ����m�����m�ķ�Χ�����жϣ�����
����m�����m�ķ�Χ�����жϣ�����![]() =��m��B��C�غϣ�������������������
=��m��B��C�غϣ�������������������![]() ����m�����m�ķ�Χ�����жϣ�
����m�����m�ķ�Χ�����жϣ�
�����������1���ߩ�![]() =��
=��![]() ��
��![]() =��
=��![]() ��
��
���������꣨��![]() ����
����![]() ����
����
��2���� ��ȥy��x2+2mx+��m2+km��3m��=0��
��ȥy��x2+2mx+��m2+km��3m��=0��
����������x�����ҽ���һ�������㣬
���=0������k��3��m=0��
������mȡ��ֵ���������dz�����
��k��3=0��
��k=3��
��3��PH=|��![]() ������
������![]() ��|=|
��|=|![]() |��
|��
��1��PH��6��
����![]() ��0ʱ����1��
��0ʱ����1��![]() ��6������1��m��4��
��6������1��m��4��
��![]() ��m��
��m��![]() ��
��
��![]() ��0ʱ��1����
��0ʱ��1����![]() ��6�����ߩ�1��m��4��
��6�����ߩ�1��m��4��
�ੁ1![]() ��
��
�ੁ1��m����![]() ��
��![]() ��m��
��m��![]() ��
��
��A����m��1��y1�����������ϣ�
��y1=����m��1��2+��2m+1������m��1��+m��m+3��=��4m��
��C����m��y3�����������ϣ�
��y3=����m��2+��2m+1������m��+m��m��3��=��4m��
��y1=y3��
����![]() ����m��1������m����
����m��1������m����![]() �������1��m�ܩ�
�������1��m�ܩ�![]() ��
��
�ੁ1��m����![]() ��
��
��ʱ���ڶԳ�������y��x���������С����ͼ1��
��y2��y1=y3��
������1��m����![]() ʱ����y2��y1=y3��
ʱ����y2��y1=y3��
����![]() =��m��1����A��B�غϣ������β������⣬������
=��m��1����A��B�غϣ������β������⣬������
����![]() ����m��1����
����m��1����![]() �ܩ�
�ܩ�![]() ʱ������
ʱ������![]() ��m�ܩ�
��m�ܩ�![]() �������1��m����
�������1��m����![]() ��
��
�ੁ![]() ��m�ܩ�
��m�ܩ�![]() ��
��
��ʱ���ڶԳ������࣬y��x���������С����ͼ2��
��y1=y3��y2��
������![]() ��m�ܩ�
��m�ܩ�![]() ʱ����y1=y3��y2��
ʱ����y1=y3��y2��
������![]() ��
��![]() ����m������
����m������![]() ��m��0�������1��m����
��m��0�������1��m����![]() ��
��
�ੁ![]() ��m����
��m����![]() ��
��
��ʱ���ڶԳ�����Ҳ�y��x�������������ͼ3��
��y2��y3=y1��
����![]() =��m��B��C�غϣ���������������
=��m��B��C�غϣ���������������
����![]() ����m����m��0�����
����m����m��0�����![]() ��m��
��m��![]() ��
��
��![]() ��m��
��m��![]() ��
��
��ʱ���ڶԳ�����Ҳ࣬y��x�������������ͼ4��
��y2��y3=y1��
����![]() ��m��
��m��![]() ʱ����y2��y3=y1��
ʱ����y2��y3=y1��
������������1��m����![]() ��
��![]() ��m��
��m��![]() ʱ����y2��y1=y3��
ʱ����y2��y1=y3��
��![]() ��m����
��m����![]() ʱ����y2��y1=y3��
ʱ����y2��y1=y3��




| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����䷽���ⷽ��x2-8x+7=0�����䷽��ȷ���ǣ�������
A. ��x+4��2=9 B. ��x��4��2=9 C. ��x��8��2=16 D. ��x+8��2=57
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij��װ��ר�Ű���160�������ֹ����Ƴ��£�ÿ��������2�����䡢1��������ɣ����ÿ��ÿ���ܹ���������10��������15������ôӦ����________�����˷������䣬����ʹÿ����Ƴ������䡢�����������ס�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����������һ����ζ�ɿڵIJ�Ʒ��Ϊ���˽��Ʒ���̵��Ƿ��ʺϣ���������ȡ��һ��Ʒ��������_________________ �������ղ������� ��������������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��CD�ǡ�O���ң�AB��ֱ������CD��AB������AC��AD��OD������AC=CD������B�����߽�CD���ӳ�����E��
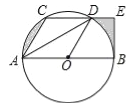
��1����֤��DAƽ�֡�CDO��
��2����AB=12����ͼ����Ӱ���ֵ��ܳ�֮�ͣ��ο����ݣ���=3.1��![]() =1.4��
=1.4��![]() =1.7����
=1.7����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪x2+x��5=0�������ʽ��x��1��2��x��x��3��+��x+2����x��2����ֵΪ ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����д�����⡰��ֱ��ƽ�У�ͬλ����ȡ�������ͽ��ۣ�
���裺_____________________��
���ۣ�_____________________��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��AB�ǡ�O��ֱ����C�ǡ�O�ϵ�һ�㣬ֱ��MN������C������A��ֱ��MN�Ĵ��ߣ�����Ϊ��D���ҡ�BAC=��CAD��
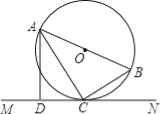
��1����֤��ֱ��MN�ǡ�O�����ߣ�
��2����CD=3����CAD=30�㣬���O�İ뾶��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com