练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

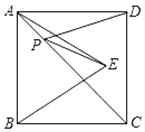
    【题目】如图，正方形ABCD的面积为12，△ABE是等边三角形，点E在正方形ABCD内，在对角线AC上有一点P，使PD+PE最小，则这个最小值为（　　）

    A. B. 2C. D. 2

    【答案】D

    【解析】

    由于点B与D关于AC对称，所以BE与AC的交点即为P点．此时PD+PE=BE最小，而BE是等边△ABE的边，BE=AB，由正方形ABCD的面积为12，可求出AB的长，从而得出结果．

    解：连接BP．

    ∵点B与D关于AC对称，
    ∴PD=PB，
    ∴PD+PE=PB+PE≥BE．．
    ∴由两点之间线段最短可知当点P为点P′处时，PD+PE有最小值，最小值=BE．

    ∵正方形ABCD的面积为12，
    ∴AB=2．
    又∵△ABE是等边三角形，
    ∴BE=AB=2．
    故所求最小值为2．
    故选：D．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】如图所示的运算程序中，若开始输入的x值为100，我们发现第1次输出的结果为50，第2次输出的结果为25，…，第2018次输出的结果为_________．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

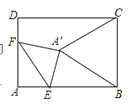
    【题目】如图,在矩形ABCD中,AB=8，AD=6,点E为AB上一点,AE=2,点F在AD上,将△AEF沿EF折叠,当折叠后点A的对应点A'恰好落在BC的垂直平分线上时,折痕EF的长为__________

    查看答案和解析>>

    科目：初中数学 来源： 题型：

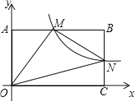
    【题目】如图，在直角坐标系中，矩形OABC的顶点O与坐标原点重合，A，C分别在坐标轴上，点B的坐标为（4，2），直线y=–x+3交AB，BC于点M，N，反比例函数的图象经过点M，N．

    （1）求反比例函数的解析式；

    （2）若点P在x轴上，且△OPM的面积与四边形BMON的面积相等，求点P的坐标．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

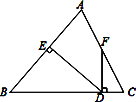
    【题目】如图所示，△ABC中，AB=BC，DE⊥AB于点E，DF⊥BC于点D，交AC于F．

    ⑴若∠AFD=155°，求∠EDF的度数；

    ⑵若点F是AC的中点，求证：∠CFD=∠B．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

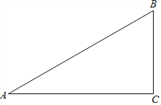
    【题目】已知：如图，在△ABC中，∠A=30°，∠B=60°．

    （1）作∠B的平分线BD，交AC于点D；

    （2）作AB的中点E（要求：尺规作图，保留作图痕迹，不必写作法和证明）；

    （3）连接DE，求证：△ADE≌△BDE．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知点O是直线AB上的一点,∠COE=，OF是∠AOE的平分线。

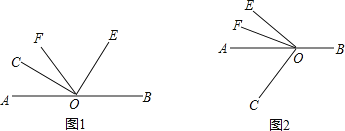
    （1）当点C,E,F在直线AB的同侧(如图1所示)时.∠AOC=时，求∠BOE和∠COF的度数，∠BOE和∠COF有什么数量关系?

    （2）当点C与点E,F在直线AB的两旁(如图2所示)时,∠AOC=，(1)中∠BOE和∠COF的数量关系的结论是否成立?请给出你的结论并说明理由；

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】数轴上A 点对应的数为﹣5，B 点在A 点右边，电子蚂蚁甲、乙在B分别以2个单位/秒、1个单位/秒的速度向左运动，电子蚂蚁丙在A 以3个单位/秒的速度向右运动．

    （1）若电子蚂蚁丙经过5秒运动到C 点，求C 点表示的数；

    （2）若它们同时出发，若丙在遇到甲后1秒遇到乙，求B 点表示的数；

    （3）在（2）的条件下，设它们同时出发的时间为t 秒，是否存在t的值，使丙到乙的距离是丙到甲的距离的2倍？若存在，求出t 值；若不存在，说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，△ABC中，∠ACB=90°，AC=BC，D是AC边上一点，AD=nCD，CE⊥BD于E交AB于F，连接DF.

    （1）如图，当BF=2AF时，求证：n=1；

    （2）如图，当DF//BC时，求的值.

    查看答案和解析>>

    同步练习册答案