
【题目】如图,△ABC中,∠ACB=90°,AC=BC,D是AC边上一点,AD=nCD,CE⊥BD于E交AB于F,连接DF.
(1)如图,当BF=2AF时,求证:n=1;
(2)如图,当DF//BC时,求![]() 的值.
的值.

【答案】(1)n=1;(2)![]()
【解析】分析:(1)作AG∥BC交CF延长线于G,则![]() ,可证明△ACG≌△CBD ,得到AG=CD .
,可证明△ACG≌△CBD ,得到AG=CD .
由AC=BC,得到AG:BC=CD:AC=![]() ,即可得到结论.
,即可得到结论.
(2)由DF∥BC,得到∠CDF=∠BCD=90°.再由∠DCE=∠EBE,得到△CDF∽△BCD,由相似三角形的性质得到DF:DC=CD:BC.可证明AD=DF.令CD=1,则DF=AD=n,BC=AC=n+1, 得到n:1=1:(n+1),解方程得到n的值.再证明△DEF∽△CDF,得到DE:EF=CD:DF=![]() ,即可得到结论.
,即可得到结论.
详解:(1)如图1,作AG∥BC交CF延长线于G,则![]() .
.
∵∠ACB=90°,∴∠ACF+∠ECB=90°.
∵CE⊥BD,∴∠ECB+∠CBE=90°,∴∠ACE=∠CBE.
∵AG∥BC,∠ACB=90°,∴∠GAC=180°-90°=90°,∴∠GAC=∠DCB.
在△ACG和△CBD中,∵∠∠GAC=∠DCB,AC=CB,∠ACE=∠CBE,∴△ACG≌△CBD ,∴AG=CD .
∵AC=BC,∴AG:BC=CD:AC=![]() ,∴AC=2CD,∴AD=CD.
,∴AC=2CD,∴AD=CD.
∵AD=nCD,∴n=1.
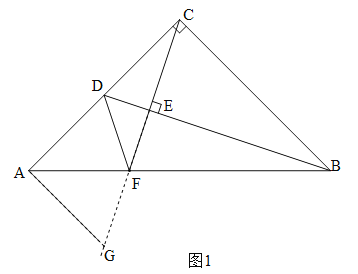
(2)如图2.
∵DF∥BC,∠ACB=90°,∴∠CDF=180°-90°=90°,∴∠CDF=∠BCD=90°.
∵∠DCE=∠EBE,∴△CDF∽△BCD,∴DF:DC=CD:BC.
∵AC=CB,∠ACB=90°,∴∠A=45°.
∵∠CDF=90°,∴∠ADF=90°,∴∠DFA=45°,∴AD=DF.令CD=1,则DF=AD=n,BC=AC=n+1, ∴n:1=1:(n+1),∴n=![]() (负数舍去),∴n=
(负数舍去),∴n=![]() .
.
∵CE⊥BD,∴∠DEF=90°.
∵∠CDF=90°,∴∠DEF=∠CDF=90°.
∵∠DFE=∠DFE,∴△DEF∽△CDF,∴DE:EF=CD:DF=![]() =
=![]() .
.


科目:初中数学 来源: 题型:
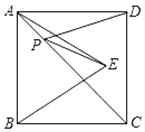
【题目】如图,正方形ABCD的面积为12,△ABE是等边三角形,点E在正方形ABCD内,在对角线AC上有一点P,使PD+PE最小,则这个最小值为( )
A. ![]() B. 2
B. 2![]() C.
C. ![]() D. 2
D. 2![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,点O是边AC上一个动点,过O作直线MN∥BC.设MN交∠ACB的平分线于点E,交∠ACB的外角平分线于点F.

(1)求证:OE=OF;
(2)若CE=12,CF=5,求OC的长;
(3)当点O在边AC上运动到什么位置时,四边形AECF是矩形?并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,∠D=90°,AB=13,BC=12,CD=4,AD=3.

求:(1)AC的长度;
(2)判断△ACB是什么三角形?并说明理由?
(3)四边形ABCD的面积。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】联合国规定每年的6月5日是“世界环境日”,为配合今年的“世界环境日”宣传活动,某实验中学课外活动小组对全校师生开展了“爱好环境,从我做起”为主题的问卷调查,并将调查结果分析整理后完成了下面的两个统计图.
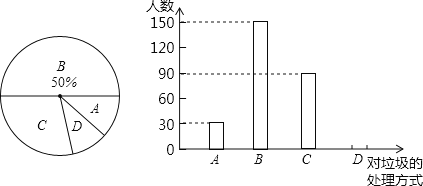
其中:
A.能将垃圾放到规定的地方,而且还会考虑垃圾的分类;
B.能将垃圾放到规定的地方,但不会考虑垃圾的分类;
C.偶尔将垃圾放在规定的地方;
D.随手乱扔垃圾.
根据以上信息回答下列问题:
(1)该校课外活动小组共调查了多少人?并补全条形统计图;
(2)如果该校共有师生3060人,那么随手乱扔垃圾的约有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某体校要从四名射击选手中选拔一名参加省体育运动会,选拔赛中每名选手连续射靶10次,他们各自的平均成绩![]() 及其方差S2如表所示:
及其方差S2如表所示:
甲 | 乙 | 丙 | 丁 | |
(环) | 8.4 | 8.6 | 8.6 | 7.6 |
S2 | 0.74 | 0.56 | 0.94 | 1.92 |
如果要选出一名成绩高且发挥稳定的选手参赛,则应选择的选手是( )
A.甲 B.乙 C.丙 D.丁
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某企业原有管理人员与营销人员的人数之比为3∶2,总人数为150,为了扩大市场,从管理人员中抽调部分人员参加营销工作,就能使营销人员是管理人员的2倍,请问应从管理人员中抽调多少人参加营销工作?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形![]() 中,
中,![]() ,
,![]() 于点
于点![]() ,动点
,动点![]() 从点
从点![]() 出发,沿
出发,沿![]() 的方向运动,到达点
的方向运动,到达点![]() 停止,设点
停止,设点![]() 运动的路程为
运动的路程为![]() ,
,![]() 的面积为
的面积为![]() ,如果
,如果![]() 与
与![]() 的函数图象如图2所示,那么
的函数图象如图2所示,那么![]() 边的长度为______.
边的长度为______.
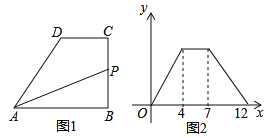
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某超市将每个进价为10元的文具袋以每个18元的销售价售出,平均每月能售出300个。市场调研表明:当每个文具袋的销售价下降1元时,其月销售量增加50个。若设每个文具袋的销售价下降m元。
(1)试用含m的式子填空:
①降价后,每个文具袋的销售价为___元;
②降价后 , 每个文具袋的利润为___元 (利润=销售价进价);
③降价后,该超市的文具袋平均每月销售量为___个;
(2)如果(1)中的m=4, 请计算该超市该月销售这种文具袋的利润是多少元?(总利润=单个利润×销售数量 )
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com