
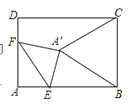
【题目】如图,在矩形ABCD中,AB=8,AD=6,点E为AB上一点,AE=2![]() ,点F在AD上,将△AEF沿EF折叠,当折叠后点A的对应点A'恰好落在BC的垂直平分线上时,折痕EF的长为__________
,点F在AD上,将△AEF沿EF折叠,当折叠后点A的对应点A'恰好落在BC的垂直平分线上时,折痕EF的长为__________
【答案】4或![]()
【解析】分析:①当AF<![]() AD时,由折叠的性质得到A′E=AE=2
AD时,由折叠的性质得到A′E=AE=2![]() ,AF=A′F,∠FA′E=∠A=90°,过E作EH⊥MN于H,由矩形的性质得到MH=AE=2
,AF=A′F,∠FA′E=∠A=90°,过E作EH⊥MN于H,由矩形的性质得到MH=AE=2![]() ,根据勾股定理得到A′H=
,根据勾股定理得到A′H=![]() ,根据勾股定理列方程即可得到结论;②当AF>
,根据勾股定理列方程即可得到结论;②当AF>![]() AD时,由折叠的性质得到A′E=AE=2 A′E2HE2,AF=A′F,∠FA′E=∠A=90°,过A′作HG∥BC交AB于G,交CD于H,根据矩形的性质得到DH=AG,HG=AD=6,根据勾股定理即可得到结论.
AD时,由折叠的性质得到A′E=AE=2 A′E2HE2,AF=A′F,∠FA′E=∠A=90°,过A′作HG∥BC交AB于G,交CD于H,根据矩形的性质得到DH=AG,HG=AD=6,根据勾股定理即可得到结论.
详解:①当AF<![]() AD时,如图1,将△AEF沿EF折叠,当折叠后点A的对应点A′恰好落在BC的垂直平分线上,
AD时,如图1,将△AEF沿EF折叠,当折叠后点A的对应点A′恰好落在BC的垂直平分线上,
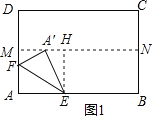
则A′E=AE=2![]() ,AF=A′F,∠FA′E=∠A=90°,
,AF=A′F,∠FA′E=∠A=90°,
设MN是BC的垂直平分线,
则AM=![]() AD=3,
AD=3,
过E作EH⊥MN于H,则四边形AEHM是矩形,
∴MH=AE=2![]() ,
,
∵A′H=![]() =
=![]() ,
,
∴A′M=![]() ,
,
∵MF2+A′M2=A′F2,
∴(3-AF)2+(![]() )2=AF2,
)2=AF2,
∴AF=2,
∴EF=![]() =4;
=4;
②当AF>![]() AD时,如图2,将△AEF沿EF折叠,当折叠后点A的对应点A′恰好落在BC的垂直平分线上,
AD时,如图2,将△AEF沿EF折叠,当折叠后点A的对应点A′恰好落在BC的垂直平分线上,
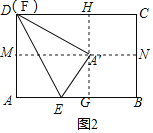
则A′E=AE=2![]() HG=3,
HG=3,
∴EG=![]() ,
,
∴DH=AG=AE+EG=3![]() ,
,
∴A′F=![]() ,
,
∴EF=![]() =4
=4![]() ,
,
综上所述,折痕EF的长为4或4![]() ,
,
故答案为:4或4![]() .
.


科目:初中数学 来源: 题型:
【题目】如图,已知正方形ABCD的面积等于25,直线a,b,c分别过A,B,C三点,且a∥b∥c,EF⊥直线c,垂足为点F交直线a于点E,若直线a,b之间的距离为3,则EF=( )
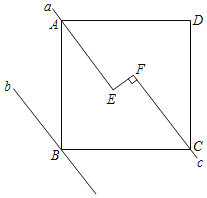
A. 1B. 2C. ![]() -3D. 5-
-3D. 5-![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】观察下列等式:
(x-1)(x+1)= x2 -1,
(x-1)(x2 +x+1)=x3 -1,
(x-1)(x3+x2 +x+1)=_________,………
(1)猜想规律(x-1)(xn +xn-1+…+x2 +x+1)=______,
(2)根据上面的结论,你能求出下面式子的结果吗?
(x20 -1)÷(x-1)=_______,
(3)已知x3+x2 +x+1=0,求x2012的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在手工制作课上,老师组织七年级(2)班的学生用硬纸制作圆柱形茶叶筒.七年级(2)班共有学生44人,其中男生人数比女生人数少2人,并且每名学生每小时剪筒身50个或剪筒底120个.
(1)七年级(2)班有男生、女生各多少人?
(2)要求一个筒身配两个筒底,为了使每小时剪出的筒身与筒底刚好配套,应该分配多少名学生剪筒身,多少名学生剪筒底?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某地电话拨号上网有两种收费方式,用户可以任意选择其中一种:第一种是计时制,0.05元/分; 第二种是包月制,69元/月(限一部个人住宅电话上网).此外,每一种上网方式都得加收通讯费0.02元/分.
(1)若小明家今年三月份上网的时间为![]() 小时,请你分别写出两种收费方式下小明家应该支付的费用;
小时,请你分别写出两种收费方式下小明家应该支付的费用;
(2)若小明估计自家一个月内上网的时间为20小时,你认为采用哪种方式较为合算?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】足球训练中,为了训练球员快速抢断转身,教练设计了折返跑训练.教练在东西方向的足球场上画了一条直线插上不同的折返旗帜,如果约定向西为正,向东为负,练习一组的行驶记录如下(单位:米):+40,-30,+50,-25,+25,-30,+15,-28,+16,-20.
(1)球员最后到达的地方在出发点的哪个方向?距出发点多远?
(2)球员训练过程中,最远处离出发点多远?
(3)球员在一组练习过程中,跑了多少米?
查看答案和解析>>
科目:初中数学 来源: 题型:
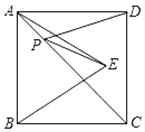
【题目】如图,正方形ABCD的面积为12,△ABE是等边三角形,点E在正方形ABCD内,在对角线AC上有一点P,使PD+PE最小,则这个最小值为( )
A. ![]() B. 2
B. 2![]() C.
C. ![]() D. 2
D. 2![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,点O是边AC上一个动点,过O作直线MN∥BC.设MN交∠ACB的平分线于点E,交∠ACB的外角平分线于点F.

(1)求证:OE=OF;
(2)若CE=12,CF=5,求OC的长;
(3)当点O在边AC上运动到什么位置时,四边形AECF是矩形?并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com