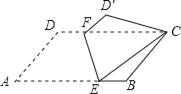
【题目】如图，将ABCD沿EF对折，使点A落在点C处，若∠A=60°，AD=4，AB=6，则AE的长为_____．
【答案】
【解析】试题解析：过点C作CG⊥AB的延长线于点G，在ABCD中，∠D=∠EBC，AD=BC，∠A=∠DCB，由于ABCD沿EF对折，∴∠D′=∠D=∠EBC，∠D′CE=∠A=∠DCB，D′C=AD=BC，∴∠D′CF+∠FCE=∠FCE+∠ECB，∴∠D′CF=∠ECB，在△D′CF与△ECB中，∠D′=∠EBC，D′C=BC，∠D′CF=∠ECB，∴△D′CF≌△ECB（ASA）
∴D′F=EB，CF=CE，∵DF=D′F，∴DF=EB，AE=CF．
设AE=x，则EB=6﹣x，CF=x，∵BC=4，∠CBG=60°，∴BG=
BC=2，由勾股定理可知：CG=
，∴EG=EB+BG=6﹣x+2=8﹣x，在△CEG中，由勾股定理可知：（8﹣x）2+（）2=x2，解得：x=AE=．故答案为：．
科目：初中数学 来源： 题型：
【题目】我国南宋著名数学家秦九韶的著作《数书九章》里记载有这样一道题：“问有沙田一块，有三斜，其中小斜五里，中斜十二里，大斜十三里，欲知为田几何？”这道题讲的是：有一块三角形沙田，三条边长分别为5里，12里，13里，问这块沙田面积有多大？题中“里”是我国市制长度单位，1里=500米，则该沙田的面积为（ ）
A. 7.5平方千米 B. 15平方千米 C. 75平方千米 D. 750平方千米
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】探究：如图1，在△ABC中，AB=AC，CF为AB边上的高，点P为BC边上任意一点，PD⊥AB，PE⊥AC，垂足分别为点D，E．求证：PD+PE=CF．
嘉嘉的证明思路：连结AP，借助△ABP与△ACP的面积和等于△ABC的面积来证明结论．
淇淇的证明思路：过点P作PG⊥CF于G，可证得PD=GF，PE=CG，则PD+PE=CF．
迁移：请参考嘉嘉或淇淇的证明思路，完成下面的问题：
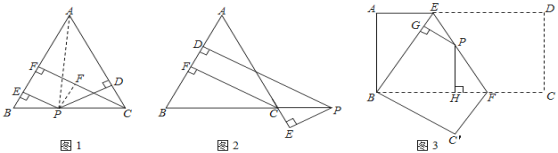
（1）如图2．当点P在BC延长线上时，其余条件不变，上面的结论还成立吗？若不成立，又存在怎样的关系？请说明理由；
（2）当点P在CB延长线上时，其余条件不变，请直接写出线段PD，PE和CF之间的数量关系．
运用：如图3，将矩形ABCD沿EF折叠，使点D落在点B处，点C落在点C′处．若点P为折痕EF上任一点，PG⊥BE于G，PH⊥BC于H，若AD=18，CF=5，直接写出PG+PH的值．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图所示的运算程序中，若开始输入的x值为100，我们发现第1次输出的结果为50，第2次输出的结果为25，…，第2018次输出的结果为_________．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】根据解答过程填空(理由或数学式) :如图，∠DAF=∠F, ∠B=∠D,那么AB与DC平行吗?
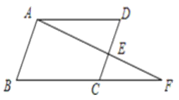
解：AB∥DC
∵∠DAF=∠F（ ），
∴AD∥BF（ ）
∴∠D=∠DCF（ ）
∵∠B=∠D（已知），
∴∠ =∠DCF（ ）
∴AB∥DC（ ）
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，数轴上线段AB=2，CD=4，点A在数轴上的数是－10，点C在数轴上表示的数是16.若线段AB以6个单位长度/秒的速度向右匀速运动，同事线段CD以2个单位长度/秒的速度向左匀速运动，点P是线段AB上一点，当点B运动到线段CD上，且BD=3PC+AP，则线段PC的长为_______.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】某商店出售一种商品，其原价为
元，现有如下两种调价方案：一种是先提价
，在此基础上又降价；另一种是先降价，在此基础上又提价.
（1）用这两种方案调价的结果是否一样？调价后的结果是不是都恢复了原价？
（2）两种调价方案改为：一种是先提价
，在此基础上又降价；另一种是先降价，在此基础上又提价，这时结果怎样？
（3）你能总结出什么规律吗？
查看答案和解析>>
科目：初中数学 来源： 题型：
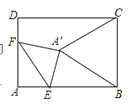
【题目】如图,在矩形ABCD中,AB=8，AD=6,点E为AB上一点,AE=2
,点F在AD上,将△AEF沿EF折叠,当折叠后点A的对应点A'恰好落在BC的垂直平分线上时,折痕EF的长为__________
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】已知点O是直线AB上的一点,∠COE=
，OF是∠AOE的平分线。
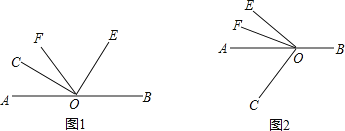
（1）当点C,E,F在直线AB的同侧(如图1所示)时.∠AOC=
时，求∠BOE和∠COF的度数，∠BOE和∠COF有什么数量关系?
（2）当点C与点E,F在直线AB的两旁(如图2所示)时,∠AOC=，(1)中∠BOE和∠COF的数量关系的结论是否成立?请给出你的结论并说明理由；
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com