
【题目】如图,数轴上线段AB=2,CD=4,点A在数轴上的数是-10,点C在数轴上表示的数是16.若线段AB以6个单位长度/秒的速度向右匀速运动,同事线段CD以2个单位长度/秒的速度向左匀速运动,点P是线段AB上一点,当点B运动到线段CD上,且BD=3PC+AP,则线段PC的长为_______.
![]()
【答案】PC=1或PC=![]()
【解析】
随着点B的运动,分别讨论当点B和点C重合、点C在点A和B之间及点A与点C重合时的情况.
设运动时间为t秒,
①∵AB=2,点A在数轴上的数是-10,
∴点B在数轴上的数是-8,
∵(8+16)÷(6+2)=3秒,
∴当t=3时,点B和点C重合,
![]()
点P在线段AB上,0<PC≤2,且BD=CD=4,
AP+3PC=AB+2PC=2+2PC,
∵BD=AP+3PC,
∴2+2PC=4,
∴PC=1;
②点A与点C重合时,(16+10) ÷(6+2)=![]() 秒,
秒,
当3<t<![]() 时,点C在点A和点B之间,0<PC<2,
时,点C在点A和点B之间,0<PC<2,
点P在线段AC上时,
![]()
BD=CD-BC=4-BC,AP+3PC=AC+2PC=AB-BC+2PC=2-BC+2PC,
∵BD=AP+3PC,
∴4-BC=2-BC+2PC,
∴PC=1;
点P在线段BC上时,
![]()
BD=CD-BC=4-BC,AP+3PC=AC+4PC=AB-BC+4PC=2-BC+4PC,
∵BD=AP+3PC,
∴4-BC=2-BC+4PC,
∴PC=![]() ;
;
③当t=![]() 时,即点A与点C重合,
时,即点A与点C重合,
![]()
0<PC≤2,BD=CD-AB=2,AP+3PC=4PC,
∵BD=AP+3PC,
∴2=4PC,
∴PC=![]() ;
;
④当点B与点D重合时,
∵BD=0,而AP+3PC≠0,
∴此时BD≠AP+3PC,不合题意,舍去.
综上所述, PC=1或PC=![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,一次函数y=kx+b的图象与反比例函数y=![]() 的图象交于A,B两点.当一次函数的值大于反比例函数的值时,自变量x的取值范围是( )
的图象交于A,B两点.当一次函数的值大于反比例函数的值时,自变量x的取值范围是( )
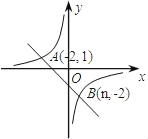
A. ﹣2<x<1 B. 0<x<1 C. x<﹣2和0<x<1 D. ﹣2<x<1和x>1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,点A在原点左侧,点B在原点右侧,且点A到原点的距离是点B到原点距离的2倍,AB=15.
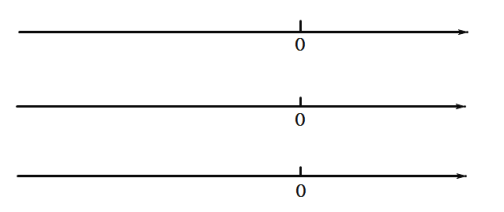
(1)点A表示的数为________,点B表示的数为________;
(2)点P从点A出发,以每秒1个单位长度的速度向点B方向运动;同时,点Q从点B出发,先向点A方向运动,当与点P重合后,马上改变方向与点P同向而行且速度始终为每秒2个单位长度。设运动时间为t秒。
①当点P与点Q重合时,求t的值;
②当点P是线段AQ的三等分点时,求t的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】观察下列等式:
(x-1)(x+1)= x2 -1,
(x-1)(x2 +x+1)=x3 -1,
(x-1)(x3+x2 +x+1)=_________,………
(1)猜想规律(x-1)(xn +xn-1+…+x2 +x+1)=______,
(2)根据上面的结论,你能求出下面式子的结果吗?
(x20 -1)÷(x-1)=_______,
(3)已知x3+x2 +x+1=0,求x2012的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某地电话拨号上网有两种收费方式,用户可以任意选择其中一种:第一种是计时制,0.05元/分; 第二种是包月制,69元/月(限一部个人住宅电话上网).此外,每一种上网方式都得加收通讯费0.02元/分.
(1)若小明家今年三月份上网的时间为![]() 小时,请你分别写出两种收费方式下小明家应该支付的费用;
小时,请你分别写出两种收费方式下小明家应该支付的费用;
(2)若小明估计自家一个月内上网的时间为20小时,你认为采用哪种方式较为合算?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=BC,以BC为直径的⊙O交AC于点D,过点D作DE⊥AB,DF⊥BC,垂足分别为E、F.
(1)求证:ED是⊙O的切线;
(2)若DF=3![]() ,cosA=
,cosA=![]() ,求⊙O的直径.
,求⊙O的直径.
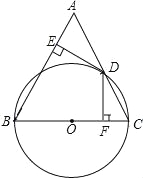
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com