
【题目】如图(1),在平行四边形ABCD中,AB=20, AD=30,∠ABC=60° ,点P从点D出发沿DC向点C匀速运动,速度为每秒3个单位长度; 同时,点Q从点B出发沿BA向点A匀速运动,速度为每秒2个单位长度.当点P停止运动时,点Q也随之停止运动. 过点P作PM⊥AD交AD于点M ,连接PQ,QM ,设运动的时间为t秒(![]() ).
).
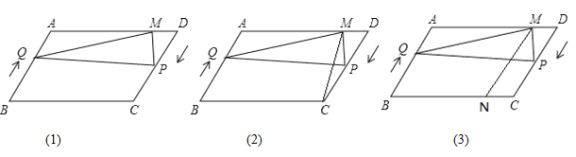
(1)当QP⊥PM时,求t的值;
(2)如图(2)连接MC,是否存在t值 ,使得△PQM的面积是平行四边形ABCD面积的![]() ? 若存在,求出对应的t值;若不存在, 请说明理由;
? 若存在,求出对应的t值;若不存在, 请说明理由;
(3)如图(3),过点M作MN//AB交于点N,是否 存在t的值, 使得点P在线段MN的垂直平分线上? 若存在, 求出对应的t的值;若不存在,请说明理由.
【答案】(1)t=4;(2)t=6;(3)t=![]() .
.
【解析】
(1)证明四边形AQPD是平行四边形,得AQ=PD,然后列方程即可解决问题.
(2)作BG⊥DA交DA的延长线于G,过点Q作QK⊥PM于K,交BG于H,求出QK,PM,构建二次函数,然后过A作AI⊥BC于I,求出AI,得到平行四边形ABCD的面积,再利用面积关系建立方程即可得出结论;
(3)根据平行四边形的性质和等腰三角形的判定和性质证明NC=PC,求出NC=PC=DM=![]() ,再根据PC+DP=CD列出方程即可解决问题.
,再根据PC+DP=CD列出方程即可解决问题.
解:(1)∵PM⊥AD,QP⊥PM,
∴PQ∥AD,
∵四边形ABCD是平行四边形,
∴AB∥CD,
∴四边形AQPD是平行四边形,
∴AQ=PD,
∴202t=3t,
∴t=4;
(2)如图,作BG⊥DA交DA的延长线于G,过点Q作QK⊥PM于K,交BG于H,则四边形GHKM是矩形,
在Rt△ABG中,∵∠G=90°,∠ABG=30°,AB=20,
∴AG=![]() AB=10,
AB=10,
在Rt△BHQ中,∵∠BHQ=90°,∠HBQ=30°,BQ=2t,
∴HQ=![]() BQ=t,
BQ=t,
在Rt△PMD中,∵∠PMD=90°,∠DPM=30°,DP=3t,
∴MD=![]() DP=
DP=![]() t,PM=
t,PM=![]() ,
,
∴QK=40![]() tt=
tt=![]() ,
,
∴S△QPM=![]() PMQK=
PMQK=![]() ×
×![]() ×(
×(![]() )=
)=![]() ,
,
过A作AI⊥BC于I,
在Rt△ABI中,AI=ABsin60°=20×![]() ,
,
∴S四边形ABCD=BCAI=30×![]() ,
,
∵△PQM的面积是ABCD面积的![]() ,
,
∴![]() ,整理得:t216t+60=0,
,整理得:t216t+60=0,
解得:t=6或t=10(舍去),
即t=6时,△PQM的面积是ABCD面积的![]() ;
;
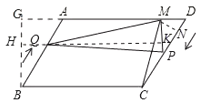
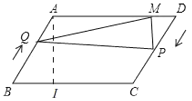
(3)连接PN,
∵点P在线段MN的垂直平分线上,
∴PM=PN,
∴∠PMN=∠PNM,
∵AB∥MN,AM∥BN,
∴四边形ABNM是平行四边形,
∴∠AMN=∠MNC=∠B=60°,
∵∠PMD=90°,∠NMD=120°,
∴∠PMN=∠PNM=∠PNC=30°,
∵∠C=120°,
∴∠CPN=30°=∠PNC,
∴NC=PC=DM=![]() ,
,
∵PC+DP=20,
∴![]() ,
,
∴t=![]() ,
,
即当t=![]() 时,点P在线段MN的垂直平分线上.
时,点P在线段MN的垂直平分线上.



科目:初中数学 来源: 题型:
【题目】长沙市教育局组织部分教师分别到A、B、C、D四个地方进行课程培训,教育局按定额购买了前往四地的车票,如图1是未制作完成的车票种类和数量的条形统计图,请根据统计图回答下列问题:
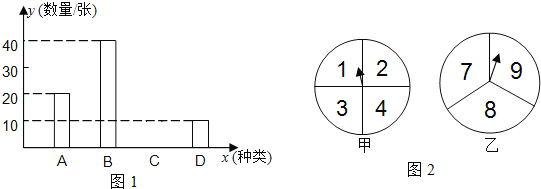
(1)若去A地的车票占全部车票的20%,求去C地的车票数,并补全条形统计图(图1);
(2)请从小到大写出这四类车票数的数字,并直接写出这四个数据的平均数和中位数;
(3)如图2,甲转盘被分成四等份且标有数字1、2、3、4,乙转盘分成三等份且标有数字7、8、9,具体规定是:同时转动两个转盘,当指针指向的两个数字之和是偶数时,李老师出去培训,否则张老师出去培训(指针指在线上重转),试用“列表法”或“树状图”的方法分析这个规定对双方是否公平.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为落实“美丽抚顺”的工作部署,市政府计划对城区道路进行了改造,现安排甲、乙两个工程队完成.已知甲队的工作效率是乙队工作效率的![]() 倍,甲队改造360米的道路比乙队改造同样长的道路少用3天.
倍,甲队改造360米的道路比乙队改造同样长的道路少用3天.
(1)甲、乙两工程队每天能改造道路的长度分别是多少米?
(2)若甲队工作一天需付费用7万元,乙队工作一天需付费用5万元,如需改造的道路全长1200米,改造总费用不超过145万元,至少安排甲队工作多少天?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数y1=﹣x+5与反比例函数y2=![]() 的图象交于A(1,m)、B(4,n)两点.
的图象交于A(1,m)、B(4,n)两点.
(1)求A、B两点的坐标和反比例函数的解析式;
(2)求△AOB的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
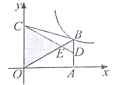
【题目】如图,四边形OABC中,AB∥OC,边OA在x轴的正半轴上,OC在y轴的正半轴上,点B在第一象限内,点D为AB的中点,CD与OB相交于点E,若△BDE、△OCE的面积分别为1和9,反比例函数y=![]() 的图象经过点B,则k=_______.
的图象经过点B,则k=_______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线y=﹣![]() x+c与x轴交于点A(3,0),与y轴交于点B,抛物线y=﹣
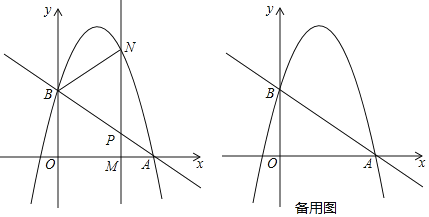
x+c与x轴交于点A(3,0),与y轴交于点B,抛物线y=﹣![]() x2+bx+c经过点A,B,M(m,0)为x轴上一动点,点M在线段OA上运动且不与O,A重合,过点M且垂直于x轴的直线与直线AB及抛物线分别交于点P,N.
x2+bx+c经过点A,B,M(m,0)为x轴上一动点,点M在线段OA上运动且不与O,A重合,过点M且垂直于x轴的直线与直线AB及抛物线分别交于点P,N.
(1)求点B的坐标和抛物线的解析式;
(2)在运动过程中,若点P为线段MN的中点,求m的值;
(3)在运动过程中,若以B,P,N为顶点的三角形与△APM相似,求点M的坐标;
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,平行四边形ABCD中,M是BC的中点,且AM=9,BD=12,AD=10,则ABCD的面积是( )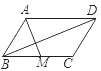
A. 30B. 36C. 54D. 72
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD中,M为BC上一点,F是AM的中点,EF⊥AM,垂足为F,交AD的延长线于点E,交DC于点N.

(1)求证:△ABM∽△EFA;
(2)若AB=12,BM=5,求DE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一位小朋友在粗糙不打滑的“Z”字形平面轨道上滚动一个半径为10cm的圆盘,如图所示,AB与CD是水平的,BC与水平面的夹角为60°,其中AB=60cm,CD=40cm,BC=40cm,那么该小朋友将圆盘从A点滚动到D点其圆心所经过的路线长为___________cm

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com