
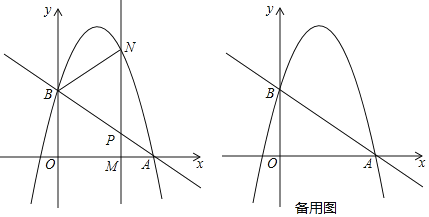
【题目】如图,直线y=﹣![]() x+c与x轴交于点A(3,0),与y轴交于点B,抛物线y=﹣
x+c与x轴交于点A(3,0),与y轴交于点B,抛物线y=﹣![]() x2+bx+c经过点A,B,M(m,0)为x轴上一动点,点M在线段OA上运动且不与O,A重合,过点M且垂直于x轴的直线与直线AB及抛物线分别交于点P,N.
x2+bx+c经过点A,B,M(m,0)为x轴上一动点,点M在线段OA上运动且不与O,A重合,过点M且垂直于x轴的直线与直线AB及抛物线分别交于点P,N.
(1)求点B的坐标和抛物线的解析式;
(2)在运动过程中,若点P为线段MN的中点,求m的值;
(3)在运动过程中,若以B,P,N为顶点的三角形与△APM相似,求点M的坐标;
【答案】(1)B(0,2),抛物线解析式为y=﹣![]() x2+
x2+![]() x+2;
x+2;
(2)m的值为![]() ;
;
(3)当以B,P,N为顶点的三角形与△APM相似时,点M的坐标为(2.5.0)或(![]() ,0).
,0).
【解析】
(1)把A点坐标代入直线解析式可求得c,则可求得B点坐标,由A、B的坐标,利用待定系数法可求得抛物线解析式;
(2)用m可表示出M、P、N的坐标,由题意可知有P为线段MN的中点,可得到关于m的方程,可求得m的值.
(3)由M点坐标可表示P、N的坐标,从而可表示出MA、MP、PN、PB的长,分∠NBP=90°和∠BNP=90°两种情况,分别利用相似三角形的性质可得到关于m的方程,可求得m的值,从而得到点M的坐标.
(1)∵y=﹣![]() x+c与x轴交于点A(3,0),与y轴交于点B,
x+c与x轴交于点A(3,0),与y轴交于点B,
∴0=﹣2+c,解得c=2,
∴B(0,2),
∵抛物线y=﹣![]() x2+bx+c经过点A,B,
x2+bx+c经过点A,B,
∴![]() ,解得
,解得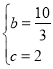 ,
,
∴抛物线解析式为y=﹣![]() x2+
x2+![]() x+2;
x+2;
(2)由(1)可知直线解析式为y=﹣![]() x+2,
x+2,
∵M(m,0)为x轴上一动点,过点M且垂直于x轴的直线与直线AB及抛物线分别交于点P,N,
∴P(m,﹣![]() m+2),N(m,﹣
m+2),N(m,﹣![]() m2+
m2+![]() m+2),
m+2),
∵P为线段MN的中点时,
∴有2(﹣![]() m+2)=﹣
m+2)=﹣![]() m2+
m2+![]() m+2,
m+2,
解得m=3(三点重合,舍去)或m=![]() .
.
故m的值为![]() .
.
(3)由(1)可知直线解析式为y=﹣![]() x+2,
x+2,
∵M(m,0)为x轴上一动点,过点M且垂直于x轴的直线与直线AB及抛物线分别交于点P,N,
∴P(m,﹣![]() m+2),N(m,﹣
m+2),N(m,﹣![]() m2+
m2+![]() m+2),
m+2),
∴PM=﹣![]() m+2,AM=3﹣m,PN=﹣
m+2,AM=3﹣m,PN=﹣![]() m2+
m2+![]() m+2﹣(﹣
m+2﹣(﹣![]() m+2)=﹣
m+2)=﹣![]() m2+4m,
m2+4m,
∵△BPN和△APM相似,且∠BPN=∠APM,
∴∠BNP=∠AMP=90°或∠NBP=∠AMP=90°,
当∠BNP=90°时,则有BN⊥MN,
∴N点的纵坐标为2,
∴﹣![]() m2+
m2+![]() m+2=2,解得m=0(舍去)或m=2.5,
m+2=2,解得m=0(舍去)或m=2.5,
∴M(2.5,0);
当∠NBP=90°时,过点N作NC⊥y轴于点C,
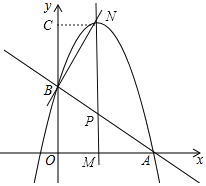
则∠NBC+∠BNC=90°,NC=m,BC=﹣![]() m2+
m2+![]() m+2﹣2=﹣
m+2﹣2=﹣![]() m2+
m2+![]() m,
m,
∵∠NBP=90°,
∴∠NBC+∠ABO=90°,
∴∠ABO=∠BNC,
∴Rt△NCB∽Rt△BOA,
∴![]() ,
,
∴![]() =
=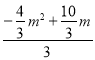 ,解得m=0(舍去)或m=
,解得m=0(舍去)或m=![]() ,
,
∴M(![]() ,0);
,0);
综上可知,当以B,P,N为顶点的三角形与△APM相似时,点M的坐标为(2.5.0)或(![]() ,0).
,0).


 新课标同步训练系列答案
新课标同步训练系列答案 一线名师口算应用题天天练一本全系列答案
一线名师口算应用题天天练一本全系列答案科目:初中数学 来源: 题型:
【题目】多多班长统计去年1~8月“书香校园”活动中全班同学的课外阅读数量(单位:本),绘制了如图折线统计图,下列说法正确的是( )

A.极差是47B.众数是42
C.中位数是58D.每月阅读数量超过40的有4个月
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的方程m x2-(m+2)x+2=0(m≠0).
(1)求证:无论m为何值时,这个方程总有两个实数根;
(2)若方程的两个实数根都是整数,求正整数m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD中, O为BD中点,以BC为边向正方形内作等边![]() BCE,连接并延长AE交CD于F,连接BD分别交CE,AF于G ,H ,下列结论:①∠CEH=45°;②GF//DE;③2OH+DH=BD;④BG=
BCE,连接并延长AE交CD于F,连接BD分别交CE,AF于G ,H ,下列结论:①∠CEH=45°;②GF//DE;③2OH+DH=BD;④BG=![]() DG;⑤
DG;⑤![]() △BEC : S△BGC=
△BEC : S△BGC=![]() .其中正确的结论是( )
.其中正确的结论是( )
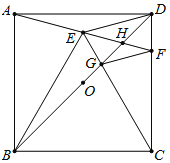
A.①②⑤B.①②④C.①②D.②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图(1),在平行四边形ABCD中,AB=20, AD=30,∠ABC=60° ,点P从点D出发沿DC向点C匀速运动,速度为每秒3个单位长度; 同时,点Q从点B出发沿BA向点A匀速运动,速度为每秒2个单位长度.当点P停止运动时,点Q也随之停止运动. 过点P作PM⊥AD交AD于点M ,连接PQ,QM ,设运动的时间为t秒(![]() ).
).
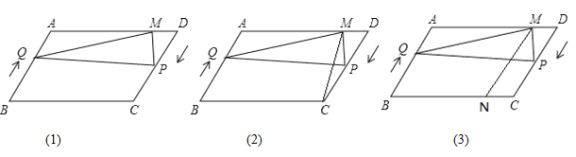
(1)当QP⊥PM时,求t的值;
(2)如图(2)连接MC,是否存在t值 ,使得△PQM的面积是平行四边形ABCD面积的![]() ? 若存在,求出对应的t值;若不存在, 请说明理由;
? 若存在,求出对应的t值;若不存在, 请说明理由;
(3)如图(3),过点M作MN//AB交于点N,是否 存在t的值, 使得点P在线段MN的垂直平分线上? 若存在, 求出对应的t的值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小美周末来到公园,发现在公园一角有一种“守株待兔”游戏.游戏设计者提供了一只兔子和一个有A,B,C,D,E五个出入口的兔笼,而且笼内的兔子从每个出入口走出兔笼的机会是均等的.规定:①玩家只能将小兔从A,B两个出入口放入:②如果小兔进入笼子后选择从开始进入的出入口离开,则可获得一只价值4元的小兔玩具,否则应付费3元.
(1)请用画树状图的方法,列举出该游戏的所有可能情况;
(2)小美得到小兔玩具的机会有多大?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知AB、AC分别为⊙O的直径和弦,D为![]() 的中点,DE垂直于AC的延长线于E,连结BC,若DE=6cm, CE=2cm,下列结论:①. DE是⊙O的切线;②. 直径AB长为20cm;③. 弦AC长为15cm;④. C为
的中点,DE垂直于AC的延长线于E,连结BC,若DE=6cm, CE=2cm,下列结论:①. DE是⊙O的切线;②. 直径AB长为20cm;③. 弦AC长为15cm;④. C为![]() 的中点.一定正确的个数是( )
的中点.一定正确的个数是( )
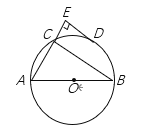
A.1B.2C.3D.4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为响应垃圾分类处理,改善生态环境,某小区将生活垃圾分成三类:厨余垃圾、可回收垃圾和其他垃圾,分别记为a,b,c,并且设置了相应的垃圾箱,“厨余垃圾”箱,“可回收垃圾”箱和“其他垃圾”箱,分别记为A,B,C
(1)小明将垃圾分装在三个袋中,任意投放,用画树状图或列表的方法求把三个袋子都放错位置的概率是多少?
(2)某学习小组为了了解居民生活垃圾分类投放的情况,现随机抽取了某天三类垃圾箱中总共100吨的生活垃圾,数据统计如表(单位:吨):
A | B | C | |
a | 40 | 10 | 10 |
b | 3 | 24 | 3 |
c | 2 | 2 | 6 |
调查发现,在“可回收垃圾”中塑料类垃圾占10%,每回收1吨塑料类垃圾可获得0.7吨二级原料,某城市每天大约产生200吨生活垃圾假设该城市每天处理投放正确的垃圾,每天大概可回收多少吨塑料类垃圾的二级原料?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,边长为2的正方形OABC的顶点A、C分别在x轴的正半轴和y轴的负半轴上,二次函数y=![]() x2+bx+c的图象经过B、C两点.
x2+bx+c的图象经过B、C两点.
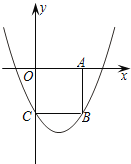
(1)求该二次函数的解析式;
(2)结合函数的图象直接写出不等式![]() x2+bx+c>0的解集.
x2+bx+c>0的解集.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com