
【题目】如图,正方形ABCD中, O为BD中点,以BC为边向正方形内作等边![]() BCE,连接并延长AE交CD于F,连接BD分别交CE,AF于G ,H ,下列结论:①∠CEH=45°;②GF//DE;③2OH+DH=BD;④BG=
BCE,连接并延长AE交CD于F,连接BD分别交CE,AF于G ,H ,下列结论:①∠CEH=45°;②GF//DE;③2OH+DH=BD;④BG=![]() DG;⑤
DG;⑤![]() △BEC : S△BGC=
△BEC : S△BGC=![]() .其中正确的结论是( )
.其中正确的结论是( )
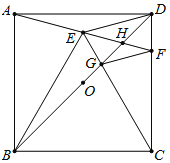
A.①②⑤B.①②④C.①②D.②③④
【答案】A
【解析】
①根据正方形的性质及等边三角形的性质求出∠BAE=∠BEA=∠CED=∠CDE=75°,∠EAD=∠EDA=15°,然后可得∠CEH=45°.
②由条件可以得出∠BDE=30°,∠DEF=30°,然后证明△DEF≌△EDG,得出DF=EG,进而得出CG=CF,求出∠CGF=75°,由∠CED=75°,就可以得出GF∥DE;
③由O为BD中点可以得出,BD=2OD=2(OH+HD),BDDH=BH,得出BH=2(OH+HD)DH=2OH+DH;
④ 设AB=BC=CD=AD=x,推出BM=![]() x,DN=
x,DN=![]() x,由
x,由![]() 可得
可得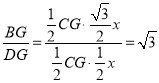 ,即可求出BG=
,即可求出BG=![]() DG.
DG.
⑤作AF的垂直平分线交AD于P,设DF=a,CE=BC=AD=![]() ,GE=DF=a,然后可得GC=
,GE=DF=a,然后可得GC=![]() ,由S△BEC:S△BGC=EC:CG,即可解决问题.
,由S△BEC:S△BGC=EC:CG,即可解决问题.
解:∵四边形ABCD是正方形,
∴AB=BC=CD=AD,∠ABC=∠BCD=∠CDA=∠DAB=90°,∠ADB=∠CDB=45°.
∵△BEC是等边三角形,
∴BC=BE=CE,∠EBC=∠BCE=∠BEC=60°,
∴AB=BE=CE=CD,∠ABE=∠DCE=30°,
∴∠BAE=∠BEA=∠CED=∠CDE=75°,
∴∠EAD=∠EDA=15°,
∴∠DEF=30°,
∴∠CEH=45°,故①正确;
∵∠EDC=75°,∠BDC=45°,
∴∠EDB=30°,
∴∠DEF=∠EDG,∠EGD=75°.
∵∠ADC=90°,∠DAF=15°,
∴∠EFD=75°,
∴∠EFD=∠EGD.
在△DEF和△EDG中,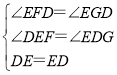 ,
,
∴△DEF≌△EDG,
∴DF=EG,
∵EC=DC,
∴ECEG=DCDF,
∴CG=CF,
∴∠CGF=∠CFG=75°,
∴∠CED=∠CGF,
∴GF∥DE,故②正确;
O为BD中点,
∴BD=2OD=2(OH+HD),
∵BDDH=BH,
∴BH=2(OH+HD)DH=2OH+2HDHD=2OH+DH.故③错误;
作BM⊥CG于M,DN⊥CE于N,
∴∠BMC=∠DNC=90°,
∴BM=sin60°BC,DN=sin30°CD,
设AB=BC=CD=AD=x,
∴BM=![]() ,DN=
,DN=![]() ,
,
∵![]() ,
,
∴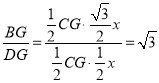 ,即BG=
,即BG=![]() DG,故④错误;
DG,故④错误;
⑤作AF的垂直平分线交AD于P,则∠DAF=∠AFP=15°,
∴∠DPF=30°,
设DF=a,
则PF=2a,DP=![]() ,
,
∴AP=PF=2a,
∴AD=![]() ,
,
∴CE=BC=AD=![]() ,GE=DF=a,
,GE=DF=a,
∴GC=![]() ,
,
∵S△BEC:S△BGC=EC:GC,
∴S△BEC:S△BGC=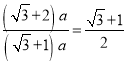 ,故⑤正确.
,故⑤正确.
综上所述,正确的是①②⑤,
故选:A.


科目:初中数学 来源: 题型:
【题目】甲、乙两同学玩转盘游戏时,把质地相同的两个盘A、B分别平均分成2份和3份,并在每一份内标有数字如图.游戏规则:甲、乙两同学分别同时转动两个转盘各1次,当转盘停止后,指针所在区域的数字之积为偶数时甲胜;数字之积为奇数时乙胜.若指针恰好在分割线上,则需要重新转动转盘.
(1)用树状图或列表的方法,求甲获胜的概率;
(2)这个游戏规则对甲、乙双方公平吗?请判断并说明理由

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知ABCD边AB,AD的长是关于x的方程x2﹣mx+4=0的两个实数根.
(1)当m为何值时,四边形ABCD是菱形?
(2)若AB的长为![]() ,那么ABCD的周长是多少?
,那么ABCD的周长是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】等腰![]() 中,
中,![]() ,点
,点![]() 是
是![]() 上一点(与
上一点(与![]() 不重合),连接
不重合),连接![]() ,将线段
,将线段![]() 绕点
绕点![]() 顺时针旋转
顺时针旋转![]() ,得到线段
,得到线段![]() .连接
.连接![]() . 探究
. 探究![]() 的度数,以及线段
的度数,以及线段![]() 与
与![]() 的数量关系.
的数量关系.
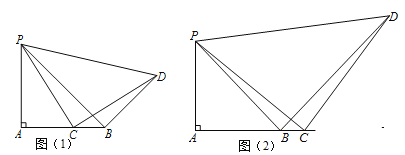
(1)尝试探究:如图(1)![]() ;
;![]() ;
;
(2)类比探索:如图(2),点![]() 在直线
在直线![]() 上,且在点
上,且在点![]() 右侧,还能得出与(1)中同样的结论么?请写出你得到的结论并证明:
右侧,还能得出与(1)中同样的结论么?请写出你得到的结论并证明:
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数y1=﹣x+5与反比例函数y2=![]() 的图象交于A(1,m)、B(4,n)两点.
的图象交于A(1,m)、B(4,n)两点.
(1)求A、B两点的坐标和反比例函数的解析式;
(2)求△AOB的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平行四边形ABCD中,将四边形折叠,使点A落在BC边上的点E处,折痕为BF.
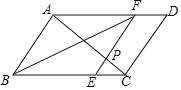
(1)求证:四边形ABEF为菱形;
(2)连接AC交EF于点P, 若CD=2CE,S△PCE=2,求![]() PAF的面积.
PAF的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线y=﹣![]() x+c与x轴交于点A(3,0),与y轴交于点B,抛物线y=﹣
x+c与x轴交于点A(3,0),与y轴交于点B,抛物线y=﹣![]() x2+bx+c经过点A,B,M(m,0)为x轴上一动点,点M在线段OA上运动且不与O,A重合,过点M且垂直于x轴的直线与直线AB及抛物线分别交于点P,N.
x2+bx+c经过点A,B,M(m,0)为x轴上一动点,点M在线段OA上运动且不与O,A重合,过点M且垂直于x轴的直线与直线AB及抛物线分别交于点P,N.
(1)求点B的坐标和抛物线的解析式;
(2)在运动过程中,若点P为线段MN的中点,求m的值;
(3)在运动过程中,若以B,P,N为顶点的三角形与△APM相似,求点M的坐标;
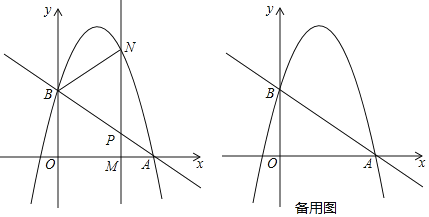
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,△ABC的三个顶点坐标分别为A(﹣2,1),B(﹣4,5),C(﹣5,2).
(1)画出△ABC关于原点O成中心对称的△A1B1C1;
(2)写出△A1B1C1的顶点坐标;
(3)求出△A1B1C1的面积.
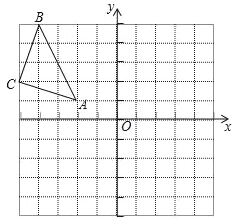
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD中,E是边AD上一点,将△ABE绕点A按逆时针方向旋转90°到△ADF的位置.已知AF=5,BE=13.
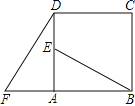
(1)求DE的长度;
(2)BE与DF是否垂直?说明你的理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com