
【题目】如图,在平行四边形ABCD中,将四边形折叠,使点A落在BC边上的点E处,折痕为BF.
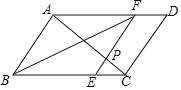
(1)求证:四边形ABEF为菱形;
(2)连接AC交EF于点P, 若CD=2CE,S△PCE=2,求![]() PAF的面积.
PAF的面积.
【答案】(1)见解析;(2)面积为8
【解析】
(1)依据条件可得AB=BE=AF=EF,即可得到四边形ABEF是菱形;
(2)首先求出AF=2CE,然后依据AF∥CE,可得△PCE∽△PAF,进而得出![]() =(
=(![]() )2=
)2=![]() ,即可求出结果.
,即可求出结果.
解:(1)如图,由折叠可知,AB=BE,AF=EF,∠1=∠2,
在平行四边形ABCD中,AD∥BC,即AF∥BE,
∴∠1=∠3,
∴∠2=∠3,
∴AB=AF,
∴AB=BE=AF=EF,
∴四边形ABEF是菱形;
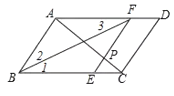
(2)在平行四边形ABCD中,CD=AB,
∵CD=2CE,AF=AB,
∴AF=2CE,
∵AF∥CE,
∴△PCE∽△PAF,
∴![]() =(
=(![]() )2=
)2=![]() ,
,
∴S△PAF=4×2=8.


科目:初中数学 来源: 题型:
【题目】某工厂现有甲种原料360千克,乙种原料290千克,计划利用这两种原料生产A、B两种产品共50件,已知生产一件A种产品用甲种原料9千克,乙种原料3千克,可获利700元;生产一件B种产品用甲种原料4千克,乙种原料10千克,可获利1200元.
(1)按要求安排A、B两种产品的生产件数,有哪几种方案?请你设计出来;
(2)设生产A、B两种产品总利润为y元,其中一种产品生产件数为x件,试写出y与x之间的函数关系式,并利用函数的性质说明那种方案获利最大?最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
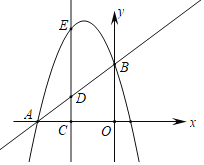
【题目】如图,已知直线y=x+4交x轴于点A,交y轴于点B,抛物线y=﹣x2+bx+c经过点A、B.
(1)求抛物线解析式;
(2)点C(m,0)是x轴上异于A、O点的一点,过点C作x轴的垂线交AB于点D,交抛物线于点E.
①当点E在直线AB上方的抛物线上时,连接AE、BE,求S△ABE的最大值;
②当DE=AD时,求m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
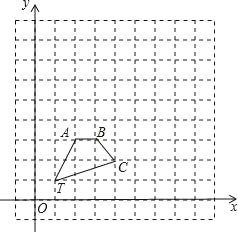
【题目】如图,在正方形网格中,四边形TABC的顶点坐标分别为T(1,1),A(2,3),B(3,3),C(4,2).
(1)以点T(1,1)为位似中心,在位似中心的同侧将四边形TABC放大为原来的2倍,放大后点A,B,C的对应点分别为A′,B′,C′画出四边形TA′B′C′;
(2)写出点A′,B′,C′的坐标:
A′ ,B′ ,C′ ;
(3)在(1)中,若D(a,b)为线段AC上任一点,则变化后点D的对应点D′的坐标为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD中, O为BD中点,以BC为边向正方形内作等边![]() BCE,连接并延长AE交CD于F,连接BD分别交CE,AF于G ,H ,下列结论:①∠CEH=45°;②GF//DE;③2OH+DH=BD;④BG=
BCE,连接并延长AE交CD于F,连接BD分别交CE,AF于G ,H ,下列结论:①∠CEH=45°;②GF//DE;③2OH+DH=BD;④BG=![]() DG;⑤
DG;⑤![]() △BEC : S△BGC=
△BEC : S△BGC=![]() .其中正确的结论是( )
.其中正确的结论是( )
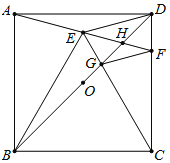
A.①②⑤B.①②④C.①②D.②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一个不透明的口袋里装有若干个除颜色外其余均相同的红、黄、蓝三种颜色的小球,其中红球2个,篮球1个,若从中任意摸出一个球,摸到球是红球的概率为![]() .
.
(1)求袋中黄球的个数;
(2)第一次任意摸出一个球(不放回),第二次再摸出一个球,求两次摸到球的颜色是红色与黄色这种组合(不考虑红、黄球顺序)的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小美周末来到公园,发现在公园一角有一种“守株待兔”游戏.游戏设计者提供了一只兔子和一个有A,B,C,D,E五个出入口的兔笼,而且笼内的兔子从每个出入口走出兔笼的机会是均等的.规定:①玩家只能将小兔从A,B两个出入口放入:②如果小兔进入笼子后选择从开始进入的出入口离开,则可获得一只价值4元的小兔玩具,否则应付费3元.
(1)请用画树状图的方法,列举出该游戏的所有可能情况;
(2)小美得到小兔玩具的机会有多大?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图△ABC≌△DEC,公共顶点为C,B在DE上,则有结论①∠ACD=∠BCE=∠ABD;②∠DAC+∠DBC=180°;③△ADC∽△BEC;④CD⊥AB,其中成立的是( )
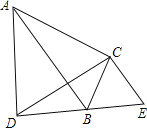
A.①②③B.只有②④C.只有①和②D.①②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,AD⊥BC于点D,BC=10cm,AD=8cm.点P从点B出发,在线段BC上以每秒3cm的速度向点C匀速运动,与此同时,垂直于AD的直线m从底边BC出发,以每秒2cm的速度沿DA方向匀速平移,分别交AB、AC、AD于E、F、H,当点P到达点C时,点P与直线m同时停止运动,设运动时间为t秒(t>0).
(1)当t=2时,连接DE、DF,求证:四边形AEDF为菱形;
(2)在整个运动过程中,问所形成的△PEF是否存在最大面积;如果存在请求出,如果不存在说明理由.
(3)是否存在某一时刻t,使△PEF为直角三角形?若存在,请求出此时刻t的值;若不存在,请说明理由.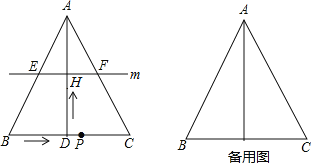
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com