
【题目】如图△ABC≌△DEC,公共顶点为C,B在DE上,则有结论①∠ACD=∠BCE=∠ABD;②∠DAC+∠DBC=180°;③△ADC∽△BEC;④CD⊥AB,其中成立的是( )
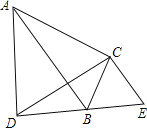
A.①②③B.只有②④C.只有①和②D.①②③④
【答案】A
【解析】
先根据全等三角形的性质,得到哪些等角和等边,然后根据这些等量条件来判断各结论是否正确.
解:∵△ABC≌△DEC,且C为公共顶点,
∴∠ABC=∠E,∠ACB=∠DCE,BC=CE;
由∠ACB=∠DCE,得∠ACD=∠BCE=∠ACB-∠BCD=∠DCE-∠BCD,
由BC=CE,得∠CBE=∠E,
∴∠ABC=∠CBE=∠E,∠ACD=∠BCE;
又∵∠ABD=180°-∠ABC-∠CBE,∠BCE=180°-∠CBE-∠E,
∴∠ABD=∠BCE=∠ACD,故①正确;
∵△ABC≌△DEC,且C为公共顶点,
∴AC=CD,即∠ACD=180°-2∠ADC;
又∵∠BCE=180°-2∠E,且∠ACD=∠BCE,
∴∠ADC=∠E=∠ABC;
由已知的全等三角形,还可得:∠BAC=∠BDC,
∴∠DAC+∠DBC=∠BAC+∠BAD+∠ABC+∠ABD=∠BAD+∠ADB+∠ABD=180°;
故②正确;
由②∠DAC+∠DBC=180°知,A、D、B、C四点共圆,
由圆周角定理知:∠ADC=∠ABC=∠E;
结合①②的证明过程知:△ADC、△BEC都是等腰三角形,且它们的底角相等,
故△ADC∽△BEC,③正确;
由于缺少条件,无法证明④的结论一定成立,故④错误;
所以正确的结论为①②③,
故选:A.


 课堂小作业系列答案
课堂小作业系列答案 黄冈小状元口算速算练习册系列答案
黄冈小状元口算速算练习册系列答案 成功训练计划系列答案
成功训练计划系列答案 倍速训练法直通中考考点系列答案
倍速训练法直通中考考点系列答案 一卷搞定系列答案
一卷搞定系列答案 名校作业本系列答案
名校作业本系列答案科目:初中数学 来源: 题型:
【题目】如图,已知二次函数![]() 的图象与y轴交于点A(0,4),与x轴交于点B,C,点C坐标为(8,0),连接AB,AC.
的图象与y轴交于点A(0,4),与x轴交于点B,C,点C坐标为(8,0),连接AB,AC.
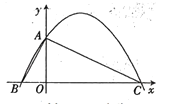
(1)请直接写出二次函数![]() 的解析式.
的解析式.
(2)判断△ABC的形状,并说明理由.
(3)若点N在x轴上运动,当以点A,N,C为顶点的三角形是等腰三角形时,请写出此时点N的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平行四边形ABCD中,将四边形折叠,使点A落在BC边上的点E处,折痕为BF.
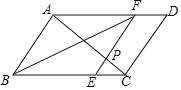
(1)求证:四边形ABEF为菱形;
(2)连接AC交EF于点P, 若CD=2CE,S△PCE=2,求![]() PAF的面积.
PAF的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2+bx+c(a≠0)的顶点和该抛物线与y轴的交点在一次函数y=kx+1(k≠0)的图象上,它的对称轴是x=1.有下列四个结论,①. abc<0; ②. a<-![]() ;③. a=-k;④. 当0<x<1时,ax+b>k,其中正确结论的个数是( )
;③. a=-k;④. 当0<x<1时,ax+b>k,其中正确结论的个数是( )
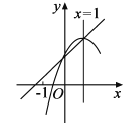
A.1;B.2C.3D.4
查看答案和解析>>
科目:初中数学 来源: 题型:
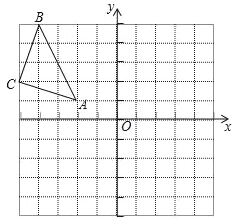
【题目】在平面直角坐标系中,△ABC的三个顶点坐标分别为A(﹣2,1),B(﹣4,5),C(﹣5,2).
(1)画出△ABC关于原点O成中心对称的△A1B1C1;
(2)写出△A1B1C1的顶点坐标;
(3)求出△A1B1C1的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图坐标系中,O(0,0),A(6,6![]() ),B(12,0),将△OAB沿直线CD折叠,使点A恰好落在线段OB上的点E处,若OE=
),B(12,0),将△OAB沿直线CD折叠,使点A恰好落在线段OB上的点E处,若OE=![]() ,则AC:AD的值是( )
,则AC:AD的值是( )
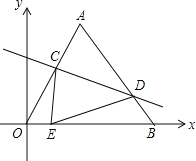
A.1:2B.2:3C.6:7D.7:8
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为宣传“扫黑除恶”专项行动,社区准备制作一幅宣传版面,喷绘时为了美观,要在矩形图案四周外围增加一圈等宽的白边,已知图案的长为2米,宽为1米,图案面积占整幅宣传版面面积的90%,若设白边的宽为x米,则根据题意可列出方程( )

A. 90%×(2+x)(1+x)=2×1 B. 90%×(2+2x)(1+2x)=2×1
C. 90%×(2﹣2x)(1﹣2x)=2×1 D. (2+2x)(1+2x)=2×1×90%
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,二次函数y=ax2+bx+c(a≠0)的图象与x轴交于A,B两点,与y轴交于C点,且对称轴为x=1,点B坐标为(﹣1,0),则下面的四个结论,其中正确的个数为( )
①2a+b=0②4a﹣2b+c<0③ac>0④当y>0时,﹣1<x<4
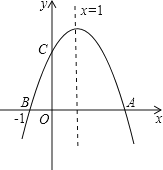
A.1个B.2个C.3个D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
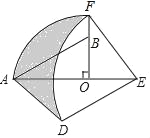
【题目】如图,在Rt△AOB中,∠AOB=90°,OA=3,OB=2,将Rt△AOB绕点O顺时针旋转90°后得Rt△FOE,将线段EF绕点E逆时针旋转90°后得线段ED,分别以O,E为圆心,OA、ED长为半径画弧AF和弧DF,连接AD,则图中阴影部分面积是_____.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com