
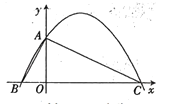
【题目】如图,已知二次函数![]() 的图象与y轴交于点A(0,4),与x轴交于点B,C,点C坐标为(8,0),连接AB,AC.
的图象与y轴交于点A(0,4),与x轴交于点B,C,点C坐标为(8,0),连接AB,AC.
(1)请直接写出二次函数![]() 的解析式.
的解析式.
(2)判断△ABC的形状,并说明理由.
(3)若点N在x轴上运动,当以点A,N,C为顶点的三角形是等腰三角形时,请写出此时点N的坐标.
【答案】(1)![]() ;(2)直角三角形,证明见解析;(3)(3,0)或(-8,0)或(
;(2)直角三角形,证明见解析;(3)(3,0)或(-8,0)或(![]() ,0)或(
,0)或(![]() ,0)
,0)
【解析】
(1)根据待定系数法即可求得;
(2)根据拋物线的解析式求得B的坐标,然后根据勾股定理分别求得AB2=20,AC2=80,BC=10然后根据勾股定理的逆定理即可证得△ABC是直角三角形
(3)分别以A.C两点为圆心,AC长为半径画弧,与m轴交于三个点,由AC的垂直平分线与c轴交于一个点,即可求得点N的坐标
(1)∵二次函数![]() 的图象与y轴交于点A(0,4),与x轴交于点B.C,点C坐标(8,0),
的图象与y轴交于点A(0,4),与x轴交于点B.C,点C坐标(8,0),
∴![]()
解得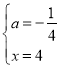
∴抛物线表达式:![]()
△ABC是直角三角形.
令y=0,则![]()
解得x1=8,x2=-2,
∴点B的坐标为(-2,0),
由已知可得,
在Rt△ABO中
AB2=BO2+AO2=22+42=20,
在Rt△AOC中
AC2=AO2+CO2=42+82=80,
又∴BC=OB+OC=2+8=10,
∴在△ABC中
AB2+AC2=20+80=102=BC2
∴△ABC是直角三角形
(3)∵A(0,4),C(8,0),
AC=![]() =4
=4![]() ,
,
①以A为圆心,以AC长为半径作圆,交轴于N,此时N的坐标为(-8,0),
②以C为圆心,以AC长为半径作圆,交x轴于N,此时N的坐标为(![]() ,0)或(
,0)或(![]() ,0)
,0)
③作AC的垂直平分线,交g轴于N,此时N的坐标为(3,0),
综上,若点N在轴上运动,当以点A、N、C为顶点的三角形是等腰三角形时,点N的坐标分别为(-8,0)、(![]() ,0)、(3,0)、
,0)、(3,0)、![]() ,0)
,0)


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
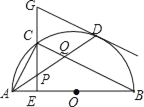
【题目】如图,在半⊙O中,AB是直径,点D是⊙O上一点,点C是![]() 的中点,CE⊥AB于点E,过点D的切线交EC的延长线于点G,连接AD,分别交CE,CB于点P,Q,连接AC,关于下列结论:①∠BAD=∠ABC;②GP=GD;③点P是△ACQ的外心;④AC2=CQCB,其中结论正确的是____.
的中点,CE⊥AB于点E,过点D的切线交EC的延长线于点G,连接AD,分别交CE,CB于点P,Q,连接AC,关于下列结论:①∠BAD=∠ABC;②GP=GD;③点P是△ACQ的外心;④AC2=CQCB,其中结论正确的是____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某工厂现有甲种原料360千克,乙种原料290千克,计划利用这两种原料生产A、B两种产品共50件,已知生产一件A种产品用甲种原料9千克,乙种原料3千克,可获利700元;生产一件B种产品用甲种原料4千克,乙种原料10千克,可获利1200元.
(1)按要求安排A、B两种产品的生产件数,有哪几种方案?请你设计出来;
(2)设生产A、B两种产品总利润为y元,其中一种产品生产件数为x件,试写出y与x之间的函数关系式,并利用函数的性质说明那种方案获利最大?最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
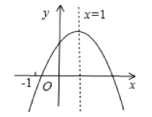
【题目】已知二次函数y=ax![]() +bx+c的图象如图所示,下列结论:①abc>0;②b<a+c;③4a+2b+c>0;④a+b+c>m(am+b)+c(m≠1的实数),其中正确的结论有 ( )
+bx+c的图象如图所示,下列结论:①abc>0;②b<a+c;③4a+2b+c>0;④a+b+c>m(am+b)+c(m≠1的实数),其中正确的结论有 ( )
A.![]() 个B.
个B.![]() 个C.
个C.![]() 个D.
个D.![]() 个
个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD与正方形A1B1C1D1关于某点中心对称,已知A, D1,D三点的坐标分别是(0,4),(0,3),(0,2).

(1)对称中心的坐标;
(2)写出顶点B, C, B1 , C1的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
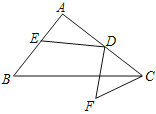
【题目】如图,在Rt△ABC中,∠A=90°,AB=6,AC=8,D为AC中点,E为AB上的动点,将ED绕点D逆时针旋转90°得到FD,连CF,则线段CF的最小值为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
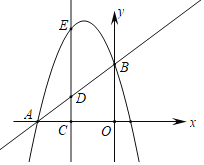
【题目】如图,已知直线y=x+4交x轴于点A,交y轴于点B,抛物线y=﹣x2+bx+c经过点A、B.
(1)求抛物线解析式;
(2)点C(m,0)是x轴上异于A、O点的一点,过点C作x轴的垂线交AB于点D,交抛物线于点E.
①当点E在直线AB上方的抛物线上时,连接AE、BE,求S△ABE的最大值;
②当DE=AD时,求m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
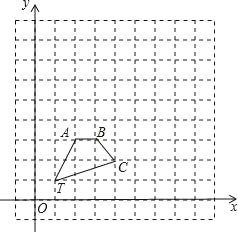
【题目】如图,在正方形网格中,四边形TABC的顶点坐标分别为T(1,1),A(2,3),B(3,3),C(4,2).
(1)以点T(1,1)为位似中心,在位似中心的同侧将四边形TABC放大为原来的2倍,放大后点A,B,C的对应点分别为A′,B′,C′画出四边形TA′B′C′;
(2)写出点A′,B′,C′的坐标:
A′ ,B′ ,C′ ;
(3)在(1)中,若D(a,b)为线段AC上任一点,则变化后点D的对应点D′的坐标为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
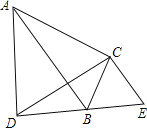
【题目】如图△ABC≌△DEC,公共顶点为C,B在DE上,则有结论①∠ACD=∠BCE=∠ABD;②∠DAC+∠DBC=180°;③△ADC∽△BEC;④CD⊥AB,其中成立的是( )
A.①②③B.只有②④C.只有①和②D.①②③④
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com